Erzwungene Schwingung eines Reihenschwingkreises

Question

Aufgabe:

Hey Leute,

um den heutigen Tag etwas abzurunden, bitte ich euch wieder um eure Hilfe.

Obwohl ich die Lösung für die Aufgabe habe... Naja es geht um den Schwingkreis...

Die Stelle wo ich hängen geblieben bin ist Rot markiert ( Doppelbruch).

Verstehe einfach nicht mit was hier erweitert wurde. Viellicht kann da jemand aushelfen.

lg

Text erkannt:

19:33 N⿻丄⿴囗十一
\( \mathrm{~ औ ) ~ ㅊ ㅓ ㄱ ㅗ} \)
Musterlősung zur 38. Übungsaufgabe
Erzwungene Schwingung eines Reihenschwingkreises
Die Schaltung wirkt als Spannungsteiler, und da sich die komplexen Widerstände bei der Reihenschaltung addieren, folgt \( \frac{U_{A}}{U_{E}}=\frac{R_{C}+R_{L}}{R_{C}+R_{L}+R_{K}}=\frac{\frac{1}{i \omega C}+i \omega L}{\frac{1}{i \omega C}+i \omega L+R_{K}}=\frac{1-\omega^{2} L C}{1-\omega^{2} L C+i \omega C R_{K}}=\frac{1}{1+\frac{i \omega C R_{K}}{1-\omega^{2} L C}}=\frac{1-\frac{i \omega C R_{K}}{1-\omega^{2} L C}}{1+\left(\frac{i \omega C R_{K}}{1-\omega^{2} L C}\right)^{2}} \)

Hieraus ergeben sich das Amplitudenverhältnis \( \frac{\hat{\theta}_{A}}{0_{E}}=\left|\frac{U_{A}}{U_{E}}\right|=\frac{1}{\sqrt{1+\left(\frac{\omega \omega_{1-\omega^{2} L C}}{}\right.} \)
\( \Delta \varphi=\tan ^{-1} \frac{\operatorname{Im}\left(\frac{U_{A}}{U_{E}}\right)}{\operatorname{Re}\left(\frac{U_{A}}{U_{E}}\right)}=\tan ^{-1}\left(-\frac{\omega C R_{K}}{1-\omega^{2} L C}\right) \). Der Verlauf beider Größen mit der Kreisfrequenz ist in Abb. 228 gezeigt. Bei \( \omega=\frac{1}{\sqrt{L C}} \), also der Resonanz des entsprechenden freien Schwingkreises, ist der Nenner unendlich und \( \hat{U}_{A}=0 \), wir haben dann also eine Antiresonanz vorliegen.

Answer 1

Hallo Bosna321,

für jemandem der aus der E-Technik kommt sticht das Problem sofort ins Auge: die konjugiert komplexe Erweiterung

Betrachte den Bruch links neben dem Bruch den Du rot markiert hast. Den musst Du nur konjugiert komplex erweitern, dann hast Du das Ergebnis. Siehe meine handgeschriebene Lösung im Bild.

Noch eine Hinweis: Wie in der E-Technik üblich, habe ich für die Imaginäre Einheit den Buchstaben J verwendet.

Gruß von hightech

Hallo Bosna321,

hier die Antwort zu Deiner Frage bezüglich dem Betrag und der Wurzel im Nenner.

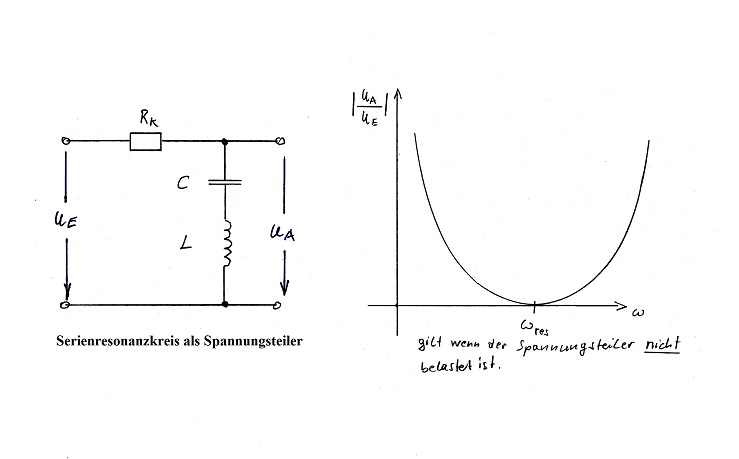
Am besten zeichnet man sich den Serienschwingkreis als Spannungsteiler auf, siehe Bild. Wenn der Spannungsteiler nicht belastet wird, dann zeigt das Amplitudenverhältnis qualitativ den Verlauf wie im Bild gezeichnet.

Das leuchtet auch ein wenn man sich die Gleichung der Übertragungsfunktion betrachtet. Am besten der 2. Bruch von links in der oberen Zeile. Sowohl für ω gegen Null, als auch für ω gegen unendlich strebt die Übertragungsfunktion gegen 1.

Hier das Bild:

Nun zu Deiner Frage mit der Wurzel im Nenner:

Am besten geht man vom 3. Bruch von links in der oberen Zeile aus:

\(\large \frac{1-ω^{2}LC}{1-ω^{2}LC+jωCR_{K}}\)

dividiert man Zähler und Nenner durch \(\large 1-ω^{2}LC\)  erhält man

\(\large \frac{1}{\frac{1}{1-ω^{2}LC}-\frac{ω^{2}LC}{1-ω^{2}LC}+j*\frac{ωCR}{1-ω^{2}LC}}\)

Nenner zusammenfassen

\(\large \frac{1}{\frac{1-ω^{2}LC}{1-ω^{2}LC}+j*\frac{ωCR}{1-ω^{2}LC}} = \frac{1}{1+j*\frac{ωCR}{1-ω^{2}LC}}\)

den Betrag der Übertragungsfunktion bilden ( nur für Nenner erfoderlich), also Wurzel aus (Quadrat des Realteil plus Quadrat des Imaginärteile)

Als Ergebnis erhält man

.\(\large \frac{1}{\sqrt{1-(\frac{ωCR}{1-ω^{2}LC})^{2}}}\)

Das Minuszeichen in der Wurzel ist kein Schreibfehler! Auf Deinem Blatt ist dort ein Pluszeichen und die imaginäre Einheit steht unter der Wurzel im Zähler des Bruchs. Das ist in der E-Technik unüblich und irriert nur. Zwar ist das mathematisch nicht falsch, da aber der Betrag gebildet werden soll, hat das Imaginärzeichen dort nichts (mehr) zu suchen. Anders ausgedrückt: der Betrag einer komplexen Größe kennt keine Imaginäreinheit.

Bei diesem Betragsausdruck, also dem Wurzelausdruck, wird das Übertragungsverhalten noch deutlicher, wenn man die Variable von Null bis Unendlichen laufen lässt.

Alles klar? Prima!

Gruß von hightech

Comments

Vielen DANK!

Was auch unverständlich bleibt ist, wie man dann daraus den Betrag bekommt bzw warum dann im Nenner die Wurzel steht? Wir hatten das jetzt schon mehrmals und ich seh es einfach nicht.

lg

---

Was auch unverständlich bleibt ist, wie man dann daraus den Betrag bekommt bzw warum dann im Nenner die Wurzel steht?

Siehe meine ergänzte Antwort.

---

Hallo Bosna321

Deine Fragen bezühlich dem Betrag und wie man auf die Wurzel im Nenner kommt, habe ich in einer Ergänzung zu der Berechnung oben, beantwortet.

Außerdem habe ich Bild eingefügt, das den Spannungsteiler mit dem Schwingkreis zeigt. In dem Bild ist auch schematisch das Amplitudenverhältnis zu sehen.

Falls es unklar sein sollte wie man auf das Vorzeichen in der Wurzel kommt, dann werde ich das gerne erklären.

Gruß von hightech

Answer 2

Hallo,

Verstehe einfach nicht mit was hier erweitert wurde

.es wurde konjugiert komplex erweitert, d.h. in diesem Fall Zähler und Nenner mit

 1 - (i * ω * C * R_K ) / (1 - ω² * L * C) multipliziert (vgl. 3. Binom: (a+b)*(a-b) = a²-b²).

Das "+" im Nenner müsste aber demnach falsch sein.

Was auch unverständlich bleibt ist, wie man dann daraus den Betrag bekommt bzw warum dann im Nenner die Wurzel steht?

a = iωCR_K / (1- ω²LC)

U_A / U_E = (1 -  a) / (1 - a²)  = (1 - a) / ((1 - a) * (1 + a)) = 1 / (1 + a )

| U_A / U_E | = 1 / √(1² + a²) = 1 / √(1 + a²)

Der absolute Betrag und damit die Länge des Zeigers errechnet sich nach dem Satz des Pythagoras.