Hallo :-)
Ich mache mal einen Freischnitt vom Gesamtsystem:
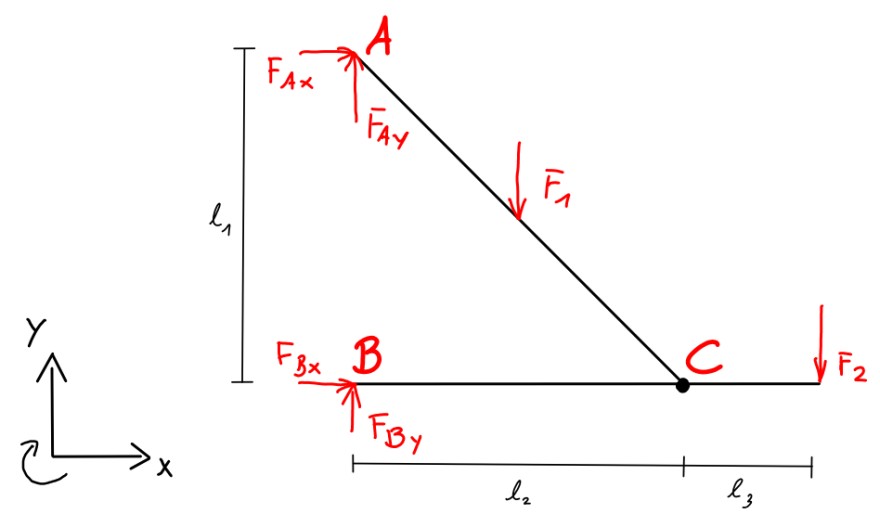
Das lässt sich in zwei Teilsysteme unterteilen:
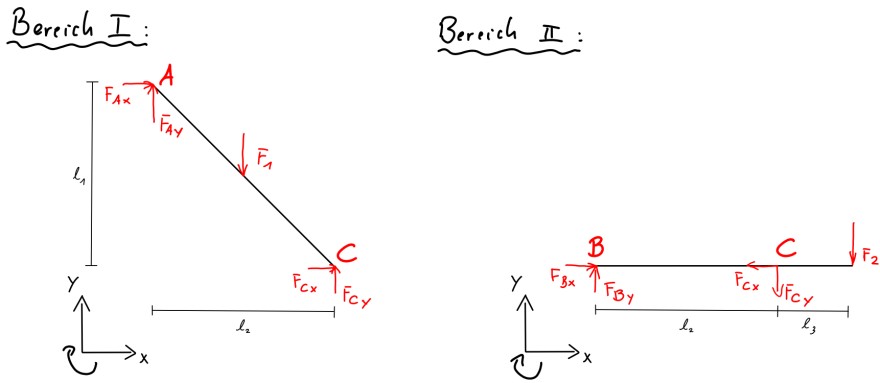
Bereich I:
\((1)\quad \sum F_x=0: \quad F_{Ax}+F_{Cx}=0\\(2)\quad \sum F_y=0:\quad F_{Ay}-F_1+F_{Cy}=0\\\qquad\qquad\qquad\qquad \Leftrightarrow \quad F_{Ay}+F_{Cy}=F_1\\(3)\quad \sum M^{(A)}=0:\quad F_1\cdot \frac{l_2}{2}-F_{Cy}\cdot l_2-F_{Cx}\cdot l_1=0\\\qquad\qquad\qquad\qquad \Leftrightarrow\quad F_{Cy}\cdot l_2+F_{Cx}\cdot l_1=F_1\cdot \frac{l_2}{2} \)
Bereich II:
\((4)\quad \sum F_x=0:\quad F_{Bx}-F_{Cx}=0\\(5)\quad \sum F_y=0:\quad F_{By}-F_{Cy}-F_2=0\\\qquad\qquad\qquad\qquad \Leftrightarrow \quad F_{By}-F_{Cy}=F_2\\(6)\quad \sum M^{(B)}=0:\quad F_{Cy}\cdot l_2+F_2\cdot (l_2+l_3)=0\\\qquad\qquad\qquad\qquad \Leftrightarrow \quad F_{Cy}\cdot l_2=-F_2\cdot (l_2+l_3)\)
Es sind also die Kräfte \(F_{Ax},F_{Bx},F_{Cx},F_{Ay},F_{By},F_{Cy}\) gesucht. Die ganzen Gleichgewichtsbedingungen von oben kannst du als Matrix-Vektor-Schreibweise umformulieren:
$$ \begin{pmatrix}1&0&1&0&0&0\\0&0&0&1&0&1\\0&0&l_1&0&0&l_2\\0&1&-1&0&0&0\\0&0&0&0&1&-1\\0&0&0&0&0&l_2\end{pmatrix}\cdot \begin{pmatrix}F_{Ax}\\F_{Bx}\\F_{Cx}\\F_{Ay}\\F_{By}\\F_{Cy}\end{pmatrix}=\begin{pmatrix}0\\F_1\\F_1\cdot \frac{l_2}{2}\\0\\F_2\\-F_2\cdot(l_2+l_3)\end{pmatrix} $$
$$\begin{array}{cccccc|c|c}F_{Ax}&F_{Bx}&F_{Cx}&F_{Ay}&F_{By}&F_{Cy} && \text{Operation}\\[4pt]\hline 1&0&1&0&0&0&0&\\[4pt]0&0&0&1&0&1&F_1&\\[4pt]0&0&l_1&0&0&l_2&F_1\cdot \frac{l_2}{2}&\text{Tausche (2) und (4)}\\[4pt]0&1&-1&0&0&0&0&\\[4pt]0&0&0&0&1&-1&F_2&\\[4pt]0&0&0&0&0&l_2&-F_2\cdot(l_2+l_3)&\\[4pt]\hline 1&0&1&0&0&0&0&\\[4pt]0&1&-1&0&0&0&0&\\[4pt]0&0&l_1&0&0&l_2&F_1\cdot \frac{l_2}{2}&(3)-(6)\\[4pt]0&0&0&1&0&1&F_1&l_2\cdot (4)-(6)\\[4pt]0&0&0&0&1&-1&F_2&l_2\cdot (5)+(6)\\[4pt]0&0&0&0&0&l_2&-F_2\cdot(l_2+l_3)\\[4pt]\hline 1&0&1&0&0&0&0&l_1\cdot (1)-(3)\\[4pt]0&1&-1&0&0&0&0&l_1\cdot (2)+(3)\\[4pt]0&0&l_1&0&0&0&F_1\cdot \frac{l_2}{2}+F_2\cdot(l_2+l_3)&\\[4pt]0&0&0&l_2&0&0&F_1\cdot l_2+F_2\cdot(l_2+l_3)&\\[4pt]0&0&0&0&l_2&0&-F_2\cdot l_3&\\[4pt]0&0&0&0&0&l_2&-F_2\cdot(l_2+l_3)\\[4pt]\hline l_1&0&0&0&0&0&-F_1\cdot \frac{l_2}{2}-F_2\cdot(l_2+l_3)&:l_1\\[4pt]0&l_1&0&0&0&0&F_1\cdot \frac{l_2}{2}+F_2\cdot(l_2+l_3)&:l_1\\[4pt]0&0&l_1&0&0&0&F_1\cdot \frac{l_2}{2}+F_2\cdot(l_2+l_3)&:l_1\\[4pt]0&0&0&l_2&0&0&F_1\cdot l_2+F_2\cdot(l_2+l_3)&:l_2\\[4pt]0&0&0&0&l_2&0&-F_2\cdot l_3&:l_2\\[4pt]0&0&0&0&0&l_2&-F_2\cdot(l_2+l_3)&:l_2\\[4pt]\hline 1&0&0&0&0&0&-F_1\cdot \frac{l_2}{2\cdot l_1}-F_2\cdot \frac{l_2+l_3}{l_1}&\\[4pt]0&1&0&0&0&0&F_1\cdot \frac{l_2}{2\cdot l_1}+F_2\cdot \frac{l_2+l_3}{l_1}&\\[4pt]0&0&1&0&0&0&F_1\cdot \frac{l_2}{2\cdot l_1}+F_2\cdot \frac{l_2+l_3}{l_1}&\\[4pt]0&0&0&1&0&0&F_1+F_2\cdot \frac{l_2+l_3}{l_2}&\\[4pt]0&0&0&0&1&0&-F_2\cdot \frac{l_3}{l_2} &\\[4pt]0&0&0&0&0&1&-F_2\cdot \frac{l_2+l_3}{l_2}& \end{array}$$