Hallo,
das Problem, das Deiner Frage zugrunde liegt kennt man auch in Hohlleiter-Übertragungstechnik. Dort kann die Phasengeschwindigkeit sogar größer als die Lichtgeschwindigkeit werden und das ist kein Widerspruch zur speziellen Relativitätstheorie! Denn die Phasengeschwindigkeit ist die Ausbreitungsgeschwindigkeit mit der sich die Phasenfronten einer Welle im Hohlleiter ausbreiten. Sie ist jedoch nicht die Signalausbreitungsgeschwindigkeit!!
Deshalb ist die bereits gegebene Antwort zu Deiner Frage falsch.
Um das zu verstehen empfehle ich Dir die Ausbreitung einer Elektromagnetischen Welle in einem Hohlleiter mal genauer anzusehen.
Ein ähnliches Phänomen oder Paradoxon ist folgendes.
Du richtest einen Laserpointer auf den Mond aus, der dort einen kleinen Lichtpunkt erzeugt (alles idealisiert). Dann drehst du dich schnell um dich selbst (z.B. in einer Sekunde um deine Achse) sodass sich der Lichtpunkt auf der Mondoberfläche bewegt. Die Frage lautet nun: Bewegt sich der Lichtpunkt auf der Mondoberfläche mit einer Geschwindigkeit, die größer ist als die Lichtgeschwindigkeit?
Gruß von hightech
Hallo,
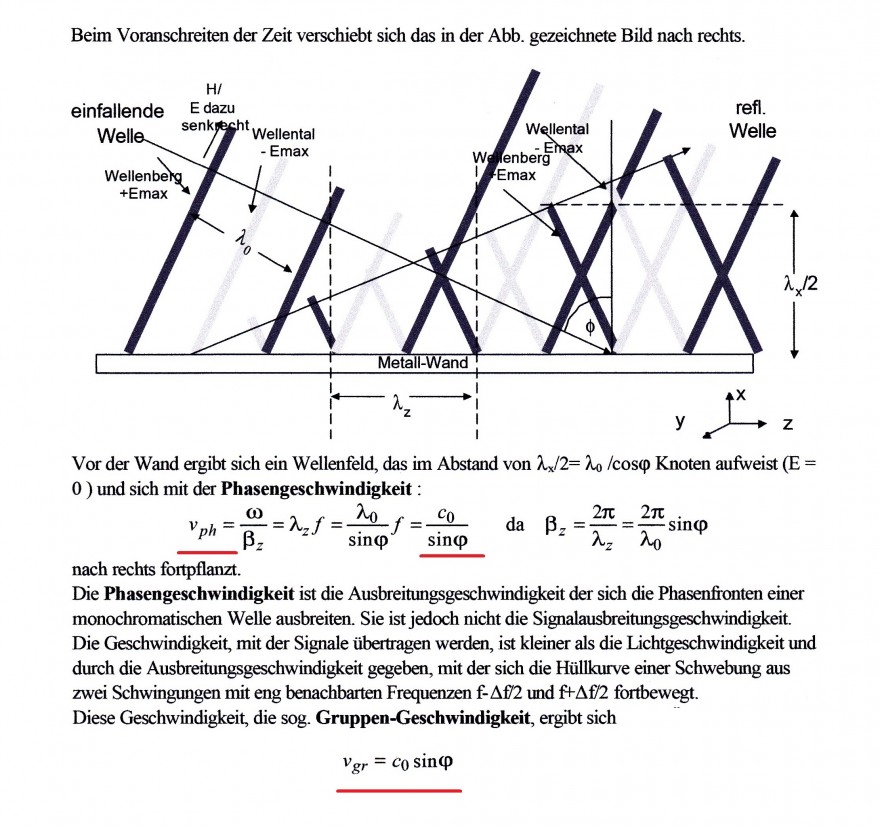
das Problem der Phasen- und Gruppengeschwindigkeit tritt auf, wenn eine ebene Welle schräg auf eine Wand trifft. Man kann nun ein Bild für die einfallende und reflektierte Wellenfront konstruieren. Dieses Bild verschiebt sich mit voranschreitender Zeit nach der Seite. Daraus lassen sich die Gleichungen für die Phasen- und Gruppengeschwindigkeit herleiten.
Als Ergebnis erhält man:
Die Phasengeschwindigkeit \(\large V_{ph}\)
\(\large V_{ph} = \frac{V}{sin(φ)}\)
Die Gruppengeschwindigkeit \(\large V_{gr}\)
\(\large V_{gr} = V*sin(φ)\)
Für den Fall dass \(\large φ = 0\) wird \(\large V_{ph} = \infty\) und \(\large V_{gr} = 0\)
Hier zur Veranschaulichung das Wellenbild einer Elektromagnetischen Welle, das im Prinzip auch für eine Akustische Welle gilt.
Gruß von hightech