Lagerreaktionen - Pendelstütze - Fachwerk

Question

Statik - Lagerreaktionen bestimmen

Hallo. Ich habe hier folgende Fachwerkaufgabe. Ich weiß grundsätzlich wie man Lagerreaktionen bestimmt. Im folgenden Beispiel ist das Fachwerk mit einem Festlager (zweiwertig) und einer Pendelstütze bzw. einem Pendelstab belastet, zumindest sehe ich das so.  

Ist das nun ein Pendelstab oder irre ich mich da? Denn wenns keiner ist dann wäre das System ja statisch unbestimmt, da 4 Unbekannte aber nur 3 Gleichgewichtsbedingungen,

Mein Ansatz für die Lagerreaktionen:

Gleichgewichtsbedingungen:

∑ F_y= 0:  B_y - F = 0  => B_y = F =1000 N

Summer der Momente um den Punkt B: - Ax *a + 2a*F = 0  => A_x = 2000N

∑ F_x =0:   B_x - A_x = 0  => B_x= A_x = 2000N

Ich wäre sehr dankbar, wenn jemand mal schnell im Kopf dies überfliegen würde, damit ich mich vergewissern kann, ob die Ergebnisse richtig sind, denn ich habe zuvor noch nicht mit Pendelstützen Lagerreaktionen ermittelt.

Danke für Eure Mühe.

Answer 1

Hallo,

lass dich nicht verwirren, oben und unten sind Festlager, also wenn du es freischneidest, hast du jeweils 2 Kräfte.

Bestimme zuerst diese Auflagerreaktionen, dann such Nullstäbe (sagen dir Nullstabsregeln was?) und dann würde ich die restlichen Stäbe freischneiden.

Um denen Freischnitt zu korrigieren, fehlt bei A noch eine vertikale Kraft und du hast bei B die Bezeichnung für B_x und B_y vertauscht.

Text erkannt:

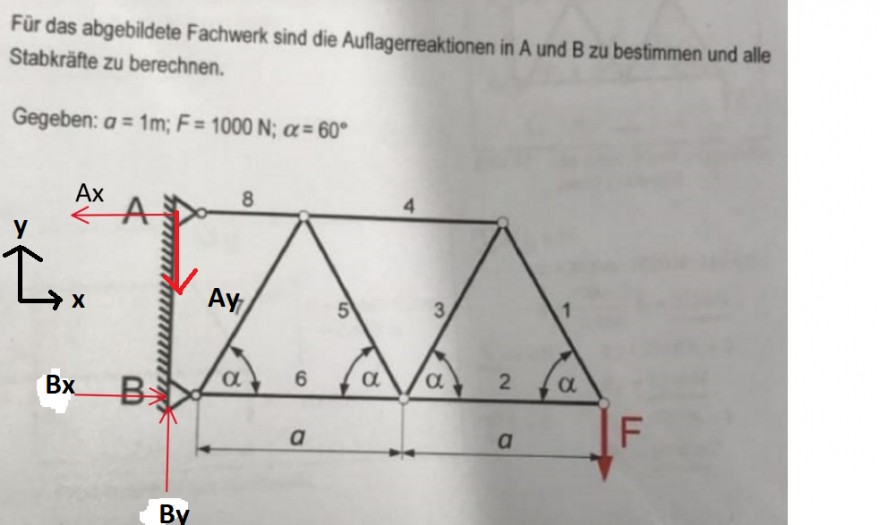
Stabkräfte zu berechnen
Gegeben: \( a=1 \mathrm{~m} ; F=1000 \mathrm{~N} ; \alpha=60^{\circ} \)

 ∑ F_x: B_x - A_x=0  → A_x=B_x

∑ F_y: B_y - A_y-F=0  → A_y=B_y-F

∑ M um den Punkt B:  A_x * s - F2a=0  → A_x=F*2*a /s

Den Hebelarm s musst du bestimmen, ist die Länge von A bis B.

Dann weißt du wie groß A_x und B_x ist.

Wie du siehst bringt dir die Gleichung 2 nichts, das heißt du musst wieder eine Momentengleichung aufstellen

Das heißt du hast 2 Momentengleichungen und eine Kräftebilant in x Richtung.