Fachwerk: Lagerkräfte berechnen und Nullstäbe erkennen

Question

Aufgaben:

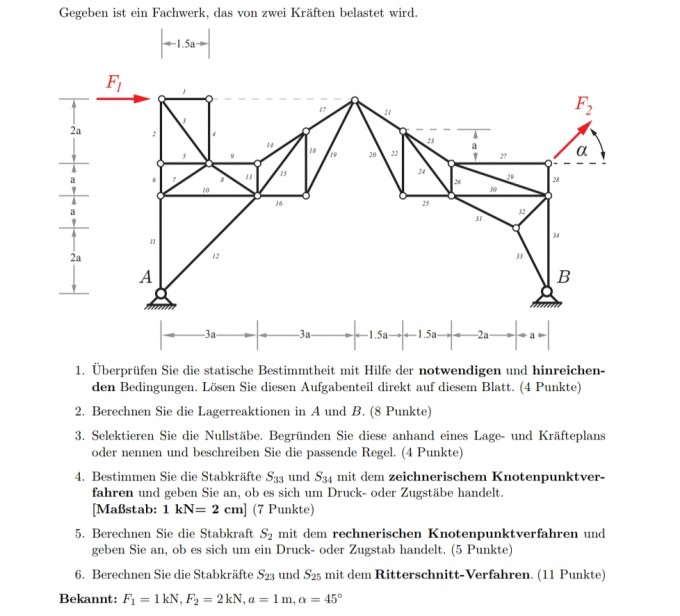
Gegeben ist ein Fachwerk, das von zwei Kräften belastet wird.

1. Überprüfen Sie die statische Bestimmtheit mit Hilfe der notwendigen und hinreichenden Bedingungen. Lösen Sie diesen Aufgabenteil direkt auf diesem Blatt. (4 Punkte)

2. Berechnen Sie die Lagerreaktionen in \( A \) und \( B \). (8 Punkte)

3. Selektieren Sie die Nullstäbe. Begründen Sie diese anhand eines Lage- und Kräfteplans oder nennen und beschreiben Sie die passende Regel. (4 Punkte)

4. Bestimmen Sie die Stabkräfte \( S_{33} \) und \( S_{34} \) mit dem zeichnerischem Knotenpunktverfahren und geben Sie an, ob es sich um Druck- oder Zugstäbe handelt.
[Maßstab: \( 1 \mathrm{kN}=2 \mathrm{~cm} \) ] (7 Punkte)

5. Berechnen Sie die Stabkraft \( S_{2} \) mit dem rechnerischen Knotenpunktverfahren und geben Sie an, ob es sich um ein Druck- oder Zugstab handelt. (5 Punkte)

6. Berechnen Sie die Stabkräfte \( S_{23} \) und \( S_{25} \) mit dem Ritterschnitt-Verfahren. (11 Punkte)
Bekannt: \( F_{1}=1 \mathrm{kN}, F_{2}=2 \mathrm{kN}, a=1 \mathrm{~m}, \alpha=45^{\circ} \)

Ansatz/Problem:

Zur Aufgabe 3:

Selektieren Sie die Nullstäbe. Begrunden Sie diese anhand eines Lage- und Kräfteplans oder nennen und beschreiben Sie die passende Regel.

Lösung: ich habe 1,4,5 als Nullstellen. Gibt es noch weitere?

Zur Aufgabe 2: Berechne die Lagerkräfte.

Könnte sie mir jemand vorrechnen?

Answer 1

Hallo Rokko,

zu 2) Bei der Berechnung der Lagerkräfte kannst Du das Teil-Fachwerk aus den Stäben 1 bis 19 sowie den Teil aus den Stäben 20 bis 34 jeweils als einen einzigen starren Körper annehmen. Beide Körper sind über ein Drehgelenk in \(C\) miteinander verbunden. Und da die Wirklinie von \(F_1\) durch den Punkt \(C\) geht, kann man das linke Teilfachwerk als einen Stab annehmen. Das hat die Konsequenz, dass die Kraft in \(A\) nur in Richtung des Stabes bzw. hier in Richtung der Geraden durch \(A\) und \(C\) verlaufen muss. D.h. \(A_y= A_x\), da \(A_x \div A_y = 1 \div 1\).

Die Kräftesumme in \(x\) und \(y\) sowie die Momentensumme um \(B\) beim rechten Teilfachwerk gibt dann

$$F_1 + A_x + F_2 \cdot \cos \alpha + B_x = 0$$ $$A_y + F_2 \cdot \sin \alpha + B_y = 0$$ $$-6 \cdot A_x - 6 \cdot A_y - 6 \cdot F_1 - 4 \cdot F_2\cos \alpha = 0$$ Beachte bei der Momentensumme, dass die Kräfte aus dem linken 'Stab' in \(C\) angreifen. Das Auflösen der Gleichungen schaffst Du alleine - oder?

zu 3) IMHO sind die Stäbe 1, 4 und 5 die einzigen Nullstäbe.

Gruß Werner

Comments

Danke. Eine frage zu 4, wie ermittle ich den Winkel von stab 33?

Könntest du mir außerdem nach dem Ritterschnitt die jeweiligen Momentsummen aufschreiben?

---

".. wie ermittle ich den Winkel von stab 33?" Zeichne Dir das Fachwerk auf Papier mit Kästchen. Die Länge eines Kästchens sei \(a\).

Der blaue Winkel \(\varphi\) oben in der Skizze muss dann sein: $$\varphi = \arctan \frac{1}{2} \approx 26,6°$$ Tipp: lass die Winkelei sein und rechne mit Verhältnissen, das ist einfacher!

Ritterschnitt folgt vielleicht morgen Abend ....

---

Guten Tag,

Könnten Sie mir zeigen wie man Punkt 5 löst?

---

zu 5) Ich nehme die beiden Stäbe \(S_2\) und \(S_3\) als Zugstäbe an und zeichne die Kräfte ein, die auf den oberen linken Knoten wirken.

Wegen der Richtung des Stabes \(S_3\) ist: $$S_{3x} \div S_{3y} = 3 \div 4$$ Kräftesumme in \(X\): $$F_1 + S_{3x} = 0 \quad \Rightarrow S_{3x} = -F_1; \space S_{3y} = -\frac43 F_1$$ $$S_3 = -F_1 \sqrt{1^2 + \left( \frac43 \right)^2 } = -\frac53 F_1$$ womit \(S_3\) ein Druckstab wäre, da die Kraft negativ ist. Kräftesumme in \(Y\): $$S_2 + S_{3y} = 0 = S_2 - \frac43 F_1 \quad \Rightarrow S_2 = \frac43 F_1$$ \(S_2\) ist ein Zugstab, da positiv.

---

Dankesehr, wäre es auch möglich gewesen, wenn man im knoten (2. Knoten der zweiten reihe) drehen würde?

---

"Könntest du mir außerdem nach dem Ritterschnitt die jeweiligen Momentsummen aufschreiben?" Ich schneide dazu das Fachwerk an der gestrichelten Linie.

Die Momentensumme um \(B\) ist

$$3a \cdot S_{25} + 3a \cdot S_{24x} - 3a \cdot S_{24y} \\ \space + 4a \cdot S_{23x} - 3a \cdot S_{23y} - 4a \cdot \frac12 \sqrt{2} F_2 = 0$$ weiter gilt

$$\frac{S_{23y}}{S_{23x}} = \frac23; \quad \frac{S_{24y}}{S_{24x}} = \frac43$$

---

"Danke sehr, wäre es auch möglich gewesen, wenn man im knoten (2. Knoten der zweiten reihe) drehen würde?" Ich verstehe die Frage nicht!?

---

Du meinst die Momentensumme um den Punkt \(P\) - oder?

 

ja - das geht auch.

---

Ja genau, danke.

---

Und wie bestimmt man nachdem Ritterschnitt Stab 23?

---

"Und wie bestimmt man nachdem Ritterschnitt Stab 23?" Indem man noch die Kräftesumme in \(x\) und \(y\) aufstellst und dann die Gleichungen auflöst. du hast 5 Unbekannte (\(S_{25y}=0)\), 2 Kräftesummen, eine Momentensumme (s.o. mein Kommentar vor 1 Stunde) und die beiden Kräfteverhältnisse.

Gruß Werner