Folgende Aufgabe:
Ein Badmintonball ist in 3 m Höhe in einem Baum hängen geblieben. Sie versuchen, ihn mit einem Basketball abzuschießen. Die horizontale Entfernung zum Badmintonball beträgt 5 m. Ihre Abwurfhöhe beträgt 2 m und Sie werfen den Basketball unter einem Winkel von 45o. Beide Bälle können als Massenpunkte betrachtet werden.
(a) Fertigen Sie eine Skizze an.
(b) Welche Anfangsgeschwindigkeit muss der Basketball haben, um den Badmintonball zu treffen?
(c) Mit welcher vertikalen und horizontalen Geschwindigkeit trifft der Basketball den Bad- mintonball?
(d) Hat der Basketball zum Zeitpunkt des Zusammentreffens den höchsten Punkt der Wurfparabel bereits überflogen? Begründen Sie Ihre Antwort.
Habe ich so versucht zu lösen:
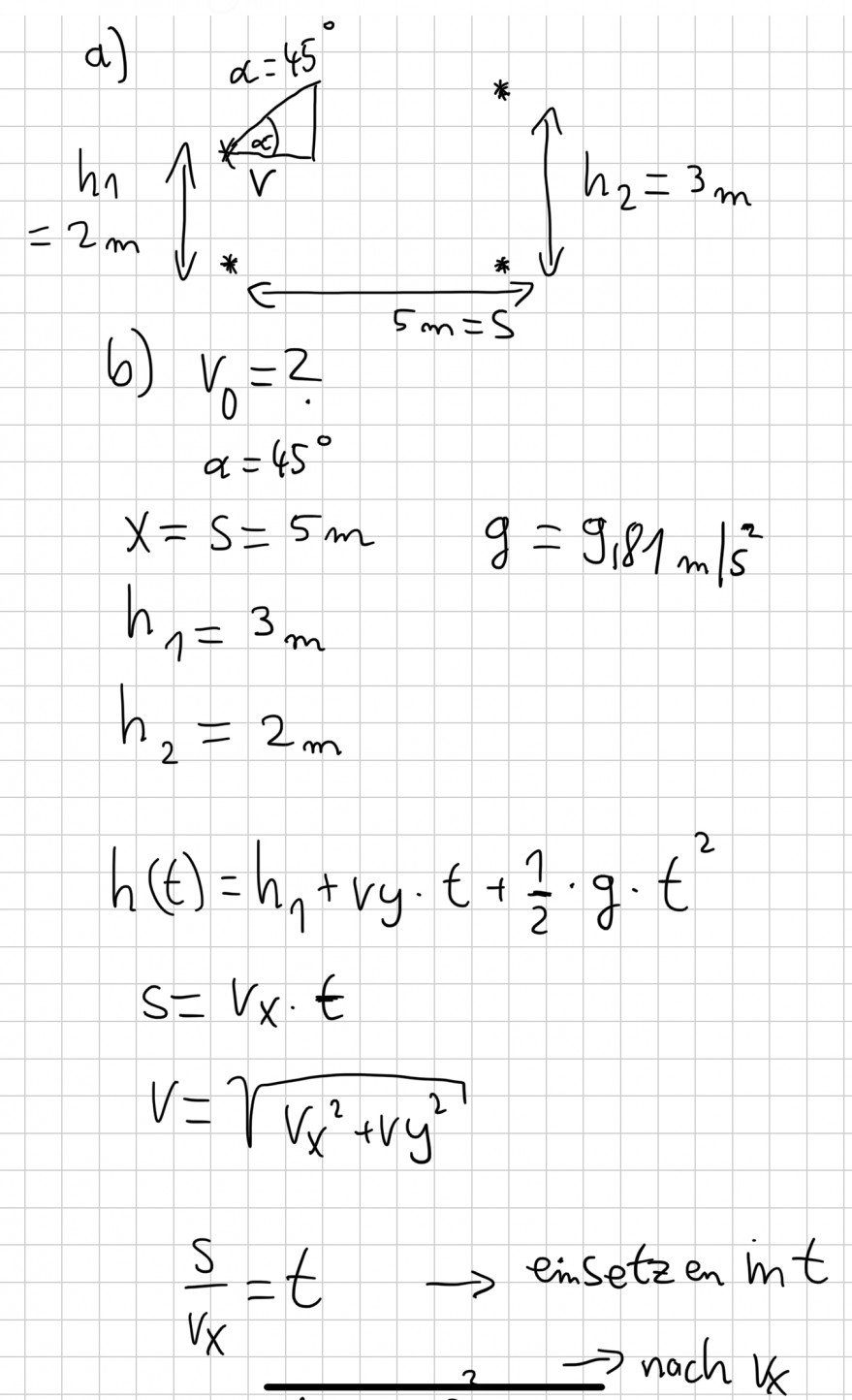
Text erkannt:
b) \( v_{n}=2 \)
\( \alpha=45^{\circ} \)
\( x=s=5 m \quad g=9,81 m \mid s^{2} \)
\( h_{1}=3 m \)
\( h_{2}=2_{m} \)
\( h(t)=h_{1}+v y \cdot t+\frac{1}{2} \cdot g \cdot t^{2} \)
\( s=v_{x} \cdot t \)
\( V=\sqrt{V_{x}^{2}+V y^{2}} \)
\( \begin{aligned} \frac{s}{v_{x}}=t & \rightarrow \text { ensetzen } m t \\ & \Rightarrow \text { nach } k \end{aligned} \)
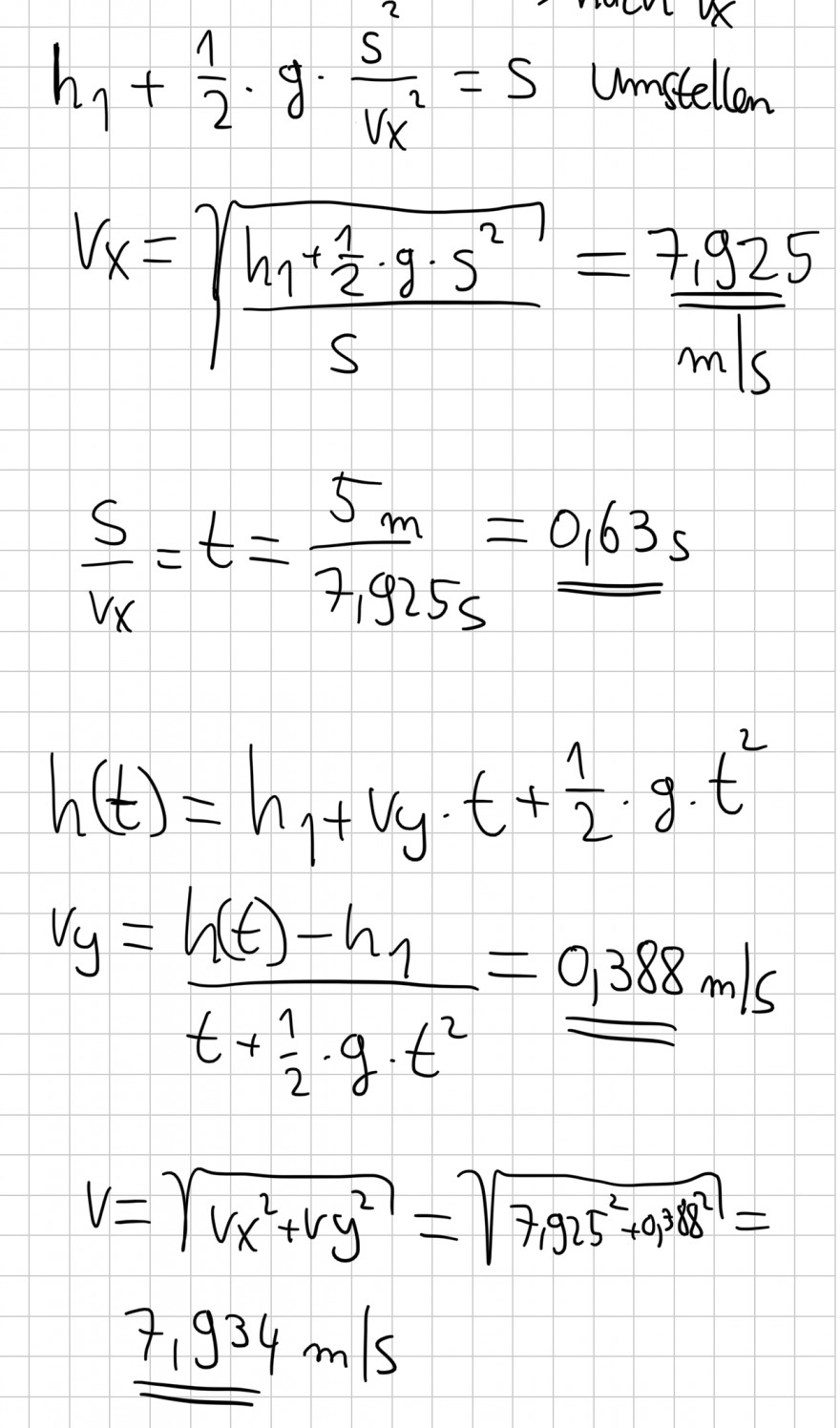
Das Ergebnis der Musterlösung liegt bei 7,83 m/s... also wo habe ich mich verrechnet?
Für c) und d) fehlen mir ebenfalls ein Ansatz...
Danke für eure Hilfe!