Hallo Lotte,
habe versucht, die Überlegungen von Ullim zu veranschaulichen.
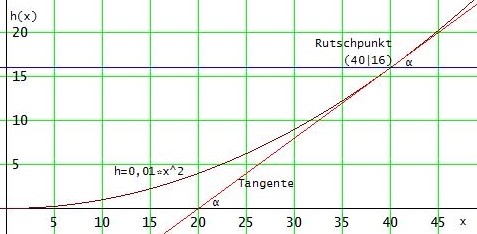
an der Felswand (=Graph) rutscht der Wanderer spätestens dann, wenn er auf der Tangente an den Graph (schiefe Ebene) rutschen würde.
Das ist der Fall, wenn die Hangabtriebskraft FH gleich (minimal größer) ist als die Haftreibungskraft FR
Von der schiefen Ebene weißt du vielleicht, dass (mit dem Steigungswinkel α) gilt:
FH = FG · sin(α) und FR = μH · FG · cos(α)
FG · sin(α) = μH · FG · cos(α) | : FG | cos(α)
sin(α)/cos(α) = μH
tan(α) = μH → tan(α) = 0,8 [ → α ≈ 38,66° ]
Andererseits ist die Tangentensteigung tan(α) gleich dem Wert der Ableitung am Berührpunkt:
h(x) = 0,001·x2 → h'(x) = 0,02·x
0,02 · x = 0,8 → x = 40 , h(40) = 16
Der Wanderer rutscht also spätestens in 16 m Höhe.
Gruß Wolfgang