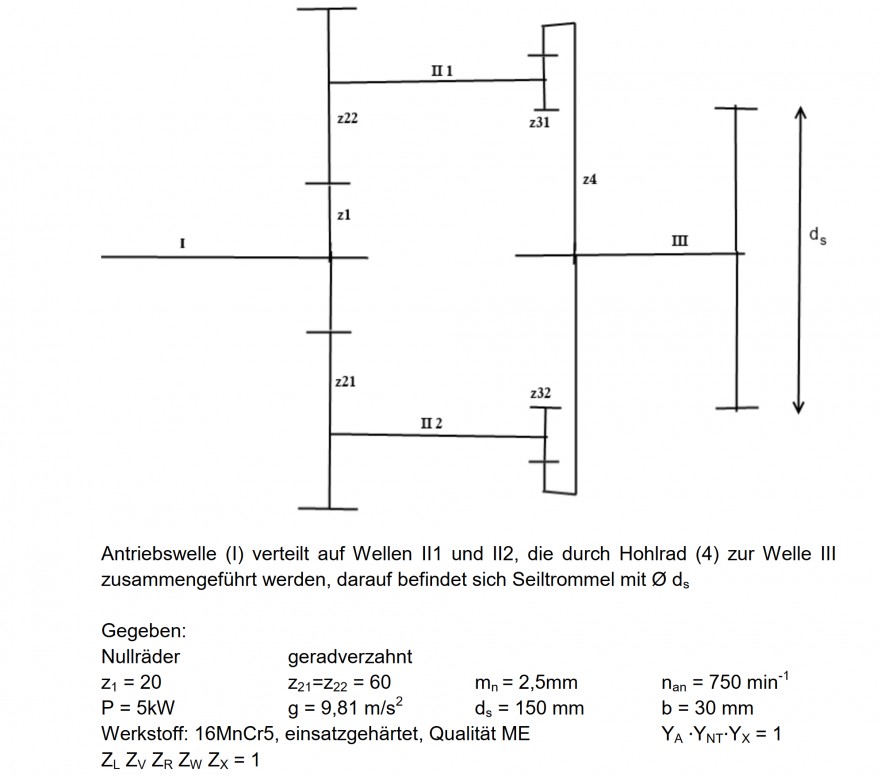
Text erkannt:
Antriebswelle (I) verteilt auf Wellen II1 und II2, die durch Hohlrad (4) zur Welle III zusammengeführt werden, darauf befindet sich Seiltrommel mit \( \varnothing \) d
Gegeben:
geradverzahnt \( z_{1}=20 \quad \mathrm{z}_{21}=\mathrm{z}_{22}=60 \quad \mathrm{m}_{\mathrm{n}}=2,5 \mathrm{mm} \quad \mathrm{n}_{\mathrm{an}}=750 \mathrm{min}^{-1} \)
\( \mathrm{P}=5 \mathrm{kW} \quad \mathrm{g}=9,81 \mathrm{m} / \mathrm{s}^{2} \quad \mathrm{d}_{\mathrm{s}}=150 \mathrm{mm} \quad \mathrm{b}=30 \mathrm{mm} \)
Werkstoff: 16MnCr5, einsatzgehärtet, Qualität ME \( Y_{A} \cdot Y_{N T} \cdot Y_{X}=1 \)
\( Z_{L} Z_{V} Z_{R} Z_{W} Z_{X}=1 \)
Problem/Ansatz:
Es soll die Masse berechnet werden, die der Kran über die Trommel auf Welle III anheben kann. Die Antriebsleistung und der Trommeldurchmesser sind gegeben.
Wenn man ein verlustfreies Getriebe annimmt, kann man ja sagen, dass an Welle III die Antriebsleistung abgegeben wird. Für die Abtriebsleistung gilt dann:
P_an = F*v.
F ist ja dann die Kraft die Seil, also F=m*g, also
P_ab = m*g*v.
Sehe ich das richtig, dass man zum Lösen der Aufgabe noch die Hubgeschwindigkeit bräuchte oder kann man die Aufgabe über einen anderen Ansatz mit den Größen aus der Angabe lösen?
Vielen Dank für die Hilfe!