Reynoldszahl bestimmen

Question

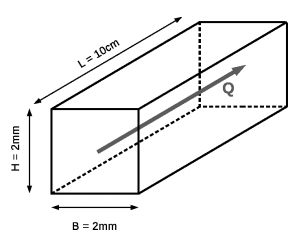
In einem Mikrofilter strömt ein Gasgemisch durch einen Kanal mit einem Volumenstrom von \( 10^{-8} 1 / \) s. Die Stoffgrößen sind: Dichte \( \rho=1 \mathrm{kg} / \mathrm{m} 3, \) dynamische Viskosität \( \eta=10^{-5} \mathrm{Pa} \) s, mittlere freie Weglange zwischen den Gasmolekillen \( \lambda=10^{-7} \mathrm{m} \) 1

Text erkannt:

1

 Lösung:

\( D_{h y d r}=\frac{4 \cdot \text { Rohrquerschnitt }}{\text { benetzter Umfang }}=\frac{4 \cdot A}{U_{b e n}} \)

D_{h y d r} = (4*4mm^2)/8mm = 2 mm

\( R e=\frac{v \cdot d_{h y d r}}{η}{ρ} \) = ?

Wie kann ich hier die Werte angeben?

Mir stehen diese Lösungsmöglichkeiten an:

[ ] Re=5000,
[ ] Re=0.05,
[ ] Re=0.0005,
[ ] Re=5 mm/s.

aber ich komme leder nicht die richtige Lösung.....?

Kann mir bitte jemand helfen...!

Liebe Grüße

Answer 1

Hallo Maike,

alle Einheiten sind in SI-Einheiten eingesetzt. Die Einheiten heben sich auf und Re ist dimensionlos.

Re = \(\dfrac{ \color{blue}{10^{-11}\frac{m^3}{s} }·0,002m·1\frac{kg}{m^3} }  { \color{blue}{4·10^{-6}m^2} ·10^{-5}Pa\text{ }s    }=0,0005\)

           Strömungsgeschwindigkeit   v = Volumenstrom/Querschnittsfläche

Gruß Wolfgang

Comments

Hallo,

ich habe nicht verstanden wie sie oben bei dem Bruch auf 10^-11 gekommen sind?

Gruß

Maike

---

ok jetzt verstanden.....

vielen dank

---

immer wieder gern :-)

---

Ich habe eine allgemeine Frage zu diese Aufgabe.

weil Re<2300 ist die Strömung doch laminar ?

und weil die Knudsenzahl Kn= λ/D <<1 ist kann man die Strömung mit der Kontinuumshypothese beschreiben oder?

Gruß

---

und

um welchen faktor müsste ich die treibende Druckdifferenz zwischen Kanalanfang und ende verändern, wenn ich den Volumenstrom durch den Mikrofilter verdoppeln möchte?

---

So sehe ich das auch.

---

und

um welchen faktor müsste ich die treibende Druckdifferenz zwischen Kanalanfang und ende verändern, wenn ich den Volumenstrom durch den Mikrofilter verdoppeln möchte?

Um 64 oder?

---

sorry ich muss den Faktor  um 4 verändern...