Hallo Leute,
Ich gucke mir gerade die Lösung folgender rein gestellter Aufgabe an. Was ist nur jetzt das Vorzeichen? In der Aufgabenstellung sind die Werte positiv. In der Lösung 2 negativ. Sind in den Gleichgewichtsbedinungen die positiven oder die negativen Werte eingeflossen? Ist die Skizze oder sind die positiven oder negativen Werte jetzt berücksichtigt? Könnte mir das jemand erklären? Ich wäre sehr dankbar...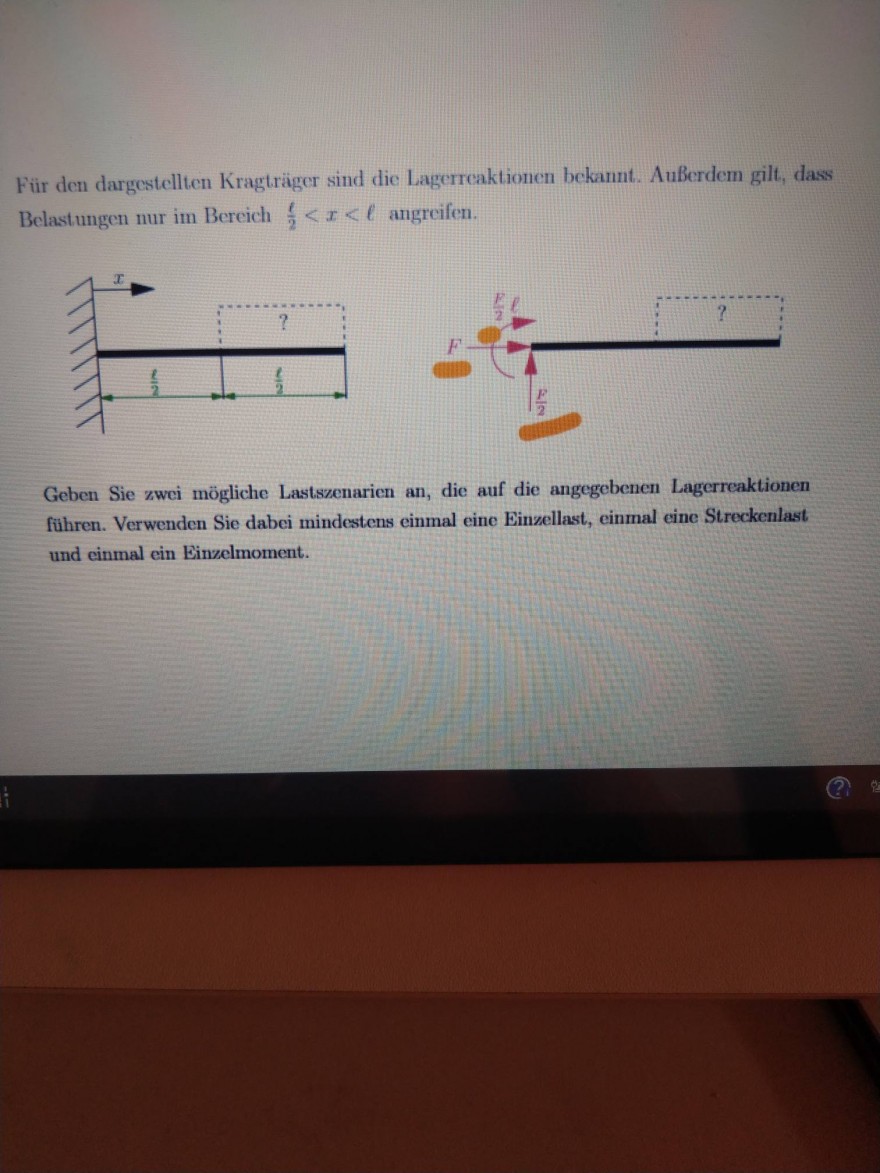
Text erkannt:
Für den dargestellten Kragtriger sind die Lagerreaktionen bckannt. AuBerdem gilt, dass Belastungen nur im Bereich \( \frac{1}{2}<x<\ell \) angreifen. \( \frac{1}{x}+1 \)
Geben Sie zwei mögliche Lastszenaricn an, die auf die angegebenen Lagerreaktionen fuhren. Verwenden Sie dabei mindestens einmal eine Einxellast, einmal eine Streckenlast und cinmal ein Einzelmoment.

Text erkannt:
Glei doch sind
die unbekannten Variablen.
Die Lagerreaktionen sind beka
Möglichkeit 1:
$$ 1 $$
2
$$ \begin{array}{l} \quad \quad \int \limits_{\frac{1}{2}}^{\frac{1}{2}} \frac{p_{0}}{\frac{1}{2} l} \\ \qquad \begin{array}{l} \sum \limits_{1} F_{x_{1}}=0=A_{x}-F_{x} \Rightarrow F_{x}=A_{x} \\ \sum \limits_{1} F_{w}=0=A_{x}+F_{x} \Rightarrow F_{x}=-A_{x}=\frac{F}{2} \end{array} \\ \sum \limits_{1}^{1} M_{1}^{1}=0=M_{1}^{1}+M_{y}-\frac{1}{2} F_{x} e \Rightarrow M_{y}=\frac{1}{2} P_{x} e-M_{y}^{A}=\frac{3}{4} F t \end{array} $$