Leistung beim Rollschuh bergauf fahren

Question

Leistung beim Rollschuh bergauf fahren

Beste Antwort

Hallo Marie,

Ich gehe mal davon aus, dass sich die Läuferin den Hang aufwärts bewegt und nur ihre Rollschuhe im Wechsel und kurzzeitig zur Seite - bzw. unter 24°. Bei 5° Steigung ergibt sich ein $F_h = G \cdot \sin 5°$ wenn $G$ das Gewicht der Läuferin ist. Beim Ausrollen wird die Läuferin die Rollschuhe sicher hangaufwärts stellen. Dann beträgt die Reibkraft $F_r = 0,1 \cdot G \cdot \cos 5°$ zumal ein Reibkoeffizient von 0,1 relativ hoch ist, da wird sicher noch der Luftwiderstand enthalten sein. ich gehe also davon aus, dass die Reibung nur in Richtung der Bewegung der Läuferin, aber nicht ausschließlich bei den Rollschuhen wirkt.

MIt der Information 0,65s für das Ausrollen und $v=4\text{m/s}$ Endgeschwindigkeit kann man nun die Gleichung für die Geschwindigkeit aufstellen - es sei $v_{\text{end}} = v_{\max} - b \cdot 0,65 \text s = 4 \frac{\text m}{\text s}$ und $b$ ist die Brensbeschleunigung mit $\begin{aligned} b &= \frac{F_h + F_r}{m} = \frac{G \cdot \sin 5° + G \cdot 0,1 \cdot \cos 5°}{m} = (\sin 5° + 0,1\cdot \cos 5°)\, g \\ &\approx 0,187\, g\end{aligned}$ wie üblich geht man von einer konstanten Beschleunigung aus. Um während der Beschleunigungsphase auf die Geschwindigkeit $v_{\max}$ zu kommen, muss sie mit $a$ beschleunigen: $v_{\max} = v_{\text{anf}} + a \cdot 0,35\text s \\ \implies a = \frac{0,65}{0,35} b = \frac{13}7 b$ Die Gesamtkraft $F_{a}$ , die sie dafür aufbringen muss ist $\begin{aligned}F_a &= a \cdot m + F_h + F_r \\&= \frac {13}7 (F_h + F_r) + F_h+F_r \\&= \frac{20}7(F_h + F_r) \\&= \frac{20}7(\sin 5° + 0,1\cdot \cos 5°)\, G \\&\approx 0,534\, G\end{aligned}$ Wie Du siehst habe ich den Wnkel von 24° nicht verwendet, da ich die Reibung nur hangaufwärts angenommen habe. IMHO käme ansonsten auch ein viel zu hoher Wert für die Leistung heraus!

Die Leistung $P_a$ während der Beschleunigungsphase ist $P_a(t) = F_a \cdot v = F_a \cdot (v_{\text{anf}} + a \cdot t)$ man kommt für $t=0$ und $m=70\text{kg}$ bereits auf einen Wert von $P_a(t)_{70} \approx 1,47 \text{kW}$ das ist schon sehr viel.

Kommst Du mit dem Rest alleine klar? Für die mittlere Leistung musst Du die Leistung $P_a(t)$ über die Zeit von $t=0$ bis $t=0,35$ integrieren und das Ergebnis durch die Summe der beiden Zeiten - also $\Delta t=1\text s$ wieder dividieren.

Nachtrag:

ich habe nochmal drüber nachgedacht. Mal angenommen, die Reibkraft soll doch gegen die Bewegung der Rollschuhe wirken. Dann ergibt sich auf der geneigten Ebene folgendes Bild:

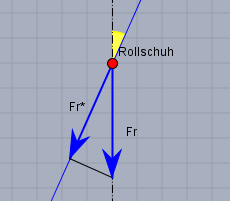
Die (Reib-)Kraft $F_r$ , die die Läuferin in Richtung ihrer Bewegung (hier im Bild senkrecht nach oben) bremst, kann man aufteilen in eine Kraft $F_r^*$ in Richtung des Rollschuhs und eine Kraft senkrecht dazu. Dann ist $F_r = \frac{F_r^*}{\cos 24°}= \frac{0,1 \cdot \cos 5°}{\cos 24°}\, G$ Die Bremsbeschleunigung $b$ ist wie oben: $\begin{aligned} b &= \frac{F_h + F_r}{m} \\&= (\sin 5° + \frac{0,1 \cdot \cos 5°}{\cos 24°} )\,g \\&\approx 0,196 \,g\end{aligned}$ und auch der Rest der Rechnung ist wie oben, nur das $F_r$ um den Faktor $1/\cos24°$ größer wird. Also ist: $\begin{aligned}F_a &= \frac {20}7 (\sin 5° + \frac{0,1 \cdot \cos 5°}{\cos 24°})\,G \\&\approx 0,561\,G \end{aligned}$ usw. wie oben beschrieben.

Falls Du noch Fragen hast, so melde Dich bitte.

Gruß Werner

Beantwortet 4 Jan 2020 von Werner-Salomon

was soll das denn dabei bedeuten, wie kann man sich im Zickzack direkt nach oben bewegen?

ich gehe mal davon aus, dass es allgemein bekannt ist, wie man sich auf Rollschuhe fort bewegt. Ich betrachte jetzt den Zustand wie er sich am Ende bzw. Anfang jedes Zyklus einstellt

Die Zeichenebene sei die Oberfläche des Hangs. Der Weg des (jetzt rechten) Rollschuhs sei die blaue Gerade. Der Schwerpunkt $S$ der Läuferin bewegt sich zu diesem Zeitpunkt schräg nach rechts vorne (in der Zeichnung oben) mit der Geschwindigkeit $v_{\text{ges}}$ . Die Vorwärtskomponente ist lt. Aufgabenstellung die $v_{\text{anf}} = 4 \text{m/s}$ .

Die Läuferin drückt ihren rechten Schuh mit der Kraft $K$ (rot) nach schräg hinten rechts und wird dadurch in die Gegenrichtung beschleunigt. Die Gegenkraft $-K$ teilt sich dabei in die waagerechte Komponente (nicht eingezeichnet) und die Vorwärtskomponent $F_a$ (s. meine Antwort), die die Läuferin nach vorn beschleunigt.

Die (in der Zeichung) waagerechte Komponente bremst das $v_x$ so weit ab, dass es zu 0 und anschließend am Ende des Zyklus den Wert $-v_x$ erreicht. Anschließend setzt sie den linken Fuß auf und hebt den rechten an und das Szenario beginnt von vorn, aber dann von links nach rechs. D.h. die Läuferin bewegt sich im Zickzack, aber im Mittel den Hang hinauf.

Frag' ruhig noch mal nach, wenn Du anderer Meinung bist. ich schließe nicht aus, dass in meinen Überlegungen noch ein Fehler drin ist.

Gruß Werner

PS.: Schade, dass wir von Marie nichts mehr lesen

Kommentiert 6 Jan 2020 von Werner-Salomon

weil die Läuferin sich nicht in Richtung ihrer Rollschuhe bewegt, sondern eben genau hangaufwärts. Ihr eigenes Gewicht G muss sie nach wie vor mit 5° den Hang hinauf schieben.

Sorry, aber die Annahme, dass die Rollschuhfahrerin direkt 5° hochfährt stimmt nicht, sie drückt sich dem rechten Rollerblade, der mit 24° nach außen gedreht ist, nach links ab, verlagert das Gewicht auf den linken Rollerblade, der ebenfalls 24° nach außen gedreht ist und fährt auf dem linken Bein nach links. Dann beginnt der Zyklus gegengleich mit dem Abdrücken mit dem linken Rollerblade nach rechts.

Pa(t)70≈1,47kW das ist schon sehr viel.

Kommst Du mit dem Rest alleine klar? Für die mittlere Leistung musst Du die Leistung Pa(t) über die Zeit von t=0 bis t=0,35 integrieren und das Ergebnis durch die Summe der beiden Zeiten - also Δt=1s wieder dividieren.

Komm mit dem Rest leider nicht so ganz klar, könntest du evtl auch die Rechnung für die mittlere Leistung zeigen? Übrigens kommt mir der Wert 1,47 kW bei dieser Steigung und Geschwindigkeitetwas hoch vor. Habe sonst immer mit der Formel P = W / t gerechnet, aber dafür müsste man noch die zurückgelegte Strecke s berechnen, könntest du das evtl auch mal zeigen?

Kommentiert 6 Jan 2020 von Marie2020

Sorry, aber die Annahme, dass die Rollschuhfahrerin direkt 5° hochfährt stimmt nicht, ...

war auch nicht so gemeint, wie geschrieben. Ich hatte mich ungenau ausgedrückt. Letztendlich wird die Fahrkurve der Läuferin eine Wellenform annehmen. ich meinte damit nur, dass sie im Mittel den hang hoch fährt. Sie wird sich also nach zwei Zyklen genau oberhalb des Punktes befinden, wo sie am Anfange der zwei Zyklen war.

könntest du evtl auch die Rechnung für die mittlere Leistung zeigen

Die Leistung $P$ wird bei konstanter Beschleunigung in den ersten 0,35s eines Zyklus immer so aussehen: $P(t) = mt + p_0 \quad m,p_0 \space \text{konstant}$ dann ist die mittlere Leistung $\overline P$ die Arbeit der Läuferin in der Beschleunigungsphase durch die Dauer eines Zyklus $\begin{aligned} \overline{P} &=\frac 1{1\text s} \int_0^{0,35\text s} P(t) \,\text dt \\&= \left. \frac 12 mt^2 + p_0t \right|_0^{0,35\text s} \cdot \frac 1{1\text s} \\&= 0,35 \left( 0,175 \text s \cdot m + p_0\right)\end{aligned}$

Übrigens kommt mir der Wert 1,47 kW bei dieser Steigung und Geschwindigkeitetwas hoch vor.

mir auch - ich erwähnte das bereits. Das liegt an dem relativ hohen Reibungskoeffizienten von 0,1. Bedenke aber, dass das nur die Leistung der Beschleunigungsphase ist. Für die mittlere Leistung (s.o.) kommt dann aber ca. nur eine Drittel dieses Wertes heraus.

Ich bin mir inzwschen auch nicht mehr sicher, ob ich bei meiner Antwort alles berücksichtigt haben. Ich hätte intuitiv erwartet, dass der Faktor $1/\cos 24°$ quadratisch eingeht. Ich denke noch drüber nach ...

Frage zum Schluß: Ist das Schule oder schon Uni?

Gruß Werner

Kommentiert 6 Jan 2020 von Werner-Salomon

Ja Uni, das Ganze ist für Biomechanik.

Die Leistung P wird bei konstanter Beschleunigung in den ersten 0,35s eines Zyklus immer so aussehen:
P(t)=mt+p0 m,p0 konstant
dann ist die mittlere Leistung P die Arbeit der Läuferin in der Beschleunigungsphase durch die Dauer eines Zyklus: P = ...

Leider kann ich das nicht ganz nachvollziehen: m ist die Masse, aber was ist p0? Und welche Formel ist das für P(t)=mt+p0? Ich dachte P = F * v oder P = W / t.

Und die Rechenschritte danach gehen mir etwas zu schnell. Woher kommt 1/1*s? Der zweite Schritt ist glaube ich eine Aufleitung um den Integral aufzulösen, wobei ich das was nach p0 t kommt nicht verstehe. Wie man dann vom 2. Schritt auf 0,35(0,175s*m+p0) kommt, kann ich leider auch nicht nachvollziehen. Sorry, hab es mit einige male angeschaut, aber komm nicht drauf.

Kommentiert 8 Jan 2020 von Marie2020

Hallo Marie,

m ist die Masse, aber was ist p0?

Upps - da hatte ich wohl zu viel vorausgesetzt. Ich hätte auch schreiben können: $P(t) = f_1 \cdot t + f_2$ und $f_1$ und $f_2$ sind irgendwelche(!) Konstanten. Wobei $f_1$ eine Größe Leistung pro Zeiteinheit und $f_2$ bereits eine Leistung ist. Ich hatte den Buchstaben $m$ gewählt, da er bei linearen Funktionen oft für die Steigung - also dem Faktor vor dem $t$ - verwendet wird.

In meiner Antwort hatte ich bereits geschrieben $P_a(t) = F_a \cdot (v_{\text{anf}} + a \cdot t)$ etwas umgeformt bekommt man $P_a(t) = F_a \cdot a \cdot t + F_a \cdot v_{\text{anf}}$ was eine lineare Funktion ist und nur das ist im folgenen von Interesse!

Und die Rechenschritte danach gehen mir etwas zu schnell. Woher kommt 1/1*s?

Die mittlere Leistung $\overline P$ (P wie 'Power') berechnet sich aus der geleisteten Arbeit $W$ (W wie 'Work') dividiert durch die Zeit $t$ , in der diese Arbeit geleistet wurde: $P = \frac{W}{t}$

Die Zeit ist die Dauer eines Zyklus und das $\cdot \frac 1{1 \text s}$ ist die Division durch die Dauer des Zyklus $0,35 \text s + 0,65 \text s = 1 \text s$ Die Arbeit wiederum wird nicht durch eine konstante Leistung aufgebracht, sondern einer Leistung, die während der Beschleunigungsphase 0,35s lang ansteigt (lineare Funktion) und anschließend 0,65s lang 0 ist. Der lineare Anstieg ist eine Konsequenz aus der Annahme, dass die Beschleunigung konstant ist. Allgemein gilt $W = P \cdot t$ (s.o.) und wenn $P$ über die Zeit nicht konstant, sondern eine Funktion der Zeit ist, so gilt $W = \int P(t) \,\text dt$ und hier gilt im besonderen $W = \int_0^{0,35\text s} P_a(t) + \underbrace{\int_{0,35 s}^{1\text s} P_a(t) \,\text dt}_{=0}$ Der zweite Teil ist das 'Rollen lassen' - hier ist die eingebrachte Leistung =0. Alles zusammen gefasst erhält man für die mittlere Leistung $\overline P = \frac Wt = \frac{\int_0^{0,35\text s} P_a(t) \,\text dt}{0,35 \text s + 0,65 \text s}$ Wenn ich nun die Größen $F_a$ , $a$ und $v_{\text{anf}}$ verwende, ergibt sich $\begin{aligned} \overline{P} &= \frac{\int_0^{0,35 \text s} F_a a t + F_a v_{\text{anf}} \,\text d t}{1 \text s} \\&= F_a \cdot \frac { \left. \frac 12 at^2 + v_{\text{anf}} t\right|_{0}^{0,35 \text s} }{1 \text s} \\&= F_a \cdot \frac {\frac 12 a (0,35 \text s)^2 + v_{\text{anf}} \cdot 0,35 \text s}{1 \text s} \\&= F_a \cdot 0,35 \cdot \left(\frac 12 a \cdot 0,35 \text s + v_{\text{anf}} \right) \\&= F_a \cdot 0,35 \cdot \left(0,175 \text s \cdot a + v_{\text{anf}} \right)\end{aligned}$ von der dritten zur vierten Zeile habe ich die Sekunde $\text s$ gekürzt und die $0,35$ ausgeklammert.

Falls noch was unklar ist, frag' ruhig noch mal nach.

Kommentiert 8 Jan 2020 von Werner-Salomon

Jetzt habe ich verstanden, wie man die Leistung mit P = F * v berechnet. Super erklärt, Danke!

Eine Frage hätte ich noch zur Beschleunigung: Für die Berechnung hast du ja gemeint, man könnte einfach annehmen die Rollschuhfahrerin würde den direkten Weg nach oben fahren, weil sie an diesem Punkt nach zwei Zyklen ist. Es ist aber so, dass ein Hang ja auch eine Kurve haben kann und man den zweiten Zyklus dann recht kurz hält, nur zum Umtreten, dann könnte man nicht mit dem direkten Weg rechnen.

Habe oben auch bei lul schon gefragt:

Wirkt bei Fh nicht auch eine Querkraft am Rollschuh, weil der Schuh wird ja nicht senkrecht zum Hang (90°) sondern nur 24° nach außen gedreht? Ohne Beschleunigung würde man nicht abrutschen, weil diese Kraft wirkt und man würde entgegen dem effektiven Winkel nach unten rollen. Verstehst du was ich meine? Wie rechnet man das?

Der effektive Winkel berechnet sich ja mit sin(effekt.Winkel) = sin(Steigung) * cos(Schuhdrehung). Wie würdest du die Rechnung damit fürs Bergauffahren aufstellen? Habe im Netz nur was zum Bergabfahren mit Ski gefunden:

http://www.dsv-datenzentrale.de/rahmentrainingsplan/xfiles_a6/120169…

http://www.dsv-datenzentrale.de/rahmentrainingsplan/xfiles_a6/120177…

Kommentiert 10 Jan 2020 von Marie2020

Hallo Marie,

ein Wort vorneweg. Deine Frage beschäftigt mich wirklich. Aber ich habe noch keine wirklich umfassende Antwort gefunden - und ich habe leider noch was anderes zu tun. Man müsste mehrere Leben haben ;-)

Das soll nicht heißen, dass Du nicht weiter fragen sollst. Das Problem interessiert mich. Und ich finde es auch gut, dass Du 'dran bleibst'.

... man könnte einfach annehmen die Rollschuhfahrerin würde den direkten Weg nach oben fahren, weil sie an diesem Punkt nach zwei Zyklen ist. Es ist aber so, dass ein Hang ja auch eine Kurve haben kann und man den zweiten Zyklus dann recht kurz hält, nur zum Umtreten, dann könnte man nicht mit dem direkten Weg rechnen.

In der Aufgabe steht: "fährt den Hang hinauf" - natürlich muss man das nicht direkt machen, aber es ist es so schon schwierig genug - und ohne Grund würde ich das Problem nicht weiter verkomplizieren. Und wenn ich schreibe 'den direkten Weg nach oben fahren' so ist zunächst nur eine Vereinfachung. Ob es zulässig ist, oder nicht kann man sich dann noch anschließend überlegen.

Wirkt bei Fh nicht auch eine Querkraft am Rollschuh, weil der Schuh wird ja nicht senkrecht zum Hang (90°) sondern nur 24° nach außen gedreht?

Ja - natürlich. Sonst käme man auch gar nicht den Hang hinauf. Wobei $F_h$ die Hangabtriebskraft ist - durch die Schrägstellung der Kufen wird dem $F_h$ entgegen gewirkt.

Der effektive Winkel berechnet sich ja mit sin(effekt.Winkel) = sin(Steigung) * cos(Schuhdrehung).

Ja - das habe ich auch raus.

Wie würdest du die Rechnung damit fürs Bergauffahren aufstellen?

Am besten gar nicht! Die Kräfte-Zeichnungen, die ich in meiner Antwort gezeichnet und gerechnet habe, liegen alle in der Hangebene. Ich rechne also nur in dieser Ebene unter der Auflage, dass das $F_h$ auf die Rollschuhläuferin wirkt und die 'Gewichtskraft' (die Normalkraft zum Hang) mit den Faktor $\cos 5° \approx 0,996$ multipliziert werden muss.

Auch hier gilt: man mache es sich möglichst einfach (nur nicht noch einfacher!) und rechne nicht in 3D sondern 'nur' in 2D(imensionen).

... Fortsetzung folgt.

Kommentiert 21 Jan 2020 von Werner-Salomon

Ah dann weiß ich auf alle Fälle schon mal, dass es doch nicht so einfach ist, das Problem zu lösen. Danke für deine Antwort, finde es super wie du mir hilfst es besser zu verstehen.

Der Winkel der Schuhdrehung spielt in dem Model dann nur für die Reibkraft eine Rolle. Wie kommt man dabei auf den Wert 1/cos(Schuhwinkel)? Und wenn man den Schuhwinkel variiert und die Rollschuhläuferin quer zum Hang laufen lässt (Schuhwinkel 90°), dann würde 0 im Nenner stehen. Die Gleichung ist so glaube ich nicht ganz richtig. Wieso nimmt man für die Reibung nicht einfach den effektiven Winkel: F,r = G * mü * cos(effektiver Winkel)?

Mit dem Schuhwinkel könnte man außerdem auch zeigen, wie sich verschiedene Läufer unterscheiden, weil wenn jemand kräftiger ist, kann er einen kleineren Winkel laufen. Ich würde den Schuhwinkel eigentlich gerne mehr berücksichtigen, so ähnlich wie in der Abbildung vom Skifahren vom DSV in dem Link, hast du die mal angeschaut?

Kommentiert 22 Jan 2020 von Marie2020

Der Winkel der Schuhdrehung spielt in dem Model dann nur für die Reibkraft eine Rolle. Wie kommt man dabei auf den Wert 1/cos(Schuhwinkel)?

Du meinst den Faktor zwischen $F_R$ und $F_R^*$ . Ich hatte oben eine Skizze eingefügt (s.o.)

Die Rollschuläufrin muss die Reibkraft in Richtung der Bewegung - hier senkrecht nach oben in der Skizze - überwinden. Die Kraft $F_R$ teilt sich in die eigentliche Reibkraft $F_R^*$ und eine Kraft senkrecht zur Bahn des Rollschuhs. Letztere habe ich nicht eingezeichnet. Ist der gelbe Winkel $\alpha$ so gilt $\cos \alpha = \frac{F_R^*}{F_R} \implies F_R = \frac{F_R^*}{\cos \alpha}$

Und wenn man den Schuhwinkel variiert und die Rollschuhläuferin quer zum Hang laufen lässt (Schuhwinkel 90°), dann würde 0 im Nenner stehen. Die Gleichung ist so glaube ich nicht ganz richtig.

Das ist sehr richtig. Eine 0 im Nemmer heißt, dass die Kraft $F_R$ gegen $\infty$ geht. Was ja auch stimmt. Wenn die Rollschuhe quer stehen ( $\to 90°$ ) kommst Du den Hang nicht hoch - egal welche Kraft Du aufwendest - jedenfalls solange die Rollschuhe nicht quer rutschen oder kaputt gehen.

Wieso nimmt man für die Reibung nicht einfach den effektiven Winkel: $F_r = G \cdot \mu \cdot \cos(\text{effektiver Winkel})$ ?

Das entspricht nicht der physikalsichen Realität. Stell Dir vor, Du ziehst einen Schlitten an einer Leine. Wenn Du horizontal ziehst $\alpha = 0°$ , dann geht die gesamte Zugkraft in die Vorwärtsbewegung. Aber da der Schlitten am Boden ist und Du etwas größer bist, wirst Du schräg nach oben ziehen. Damit geht ein Teil Deiner Zugkraft verloren. Du musst um den Faktor $1/\cos \alpha$ mehr ziehen, um die gleiche Vorwärtskraft aufzubringen. Ziehst Du senkrecht nach oben $\alpha =90°$ kannst Du den Schlitten zwar anheben, kommst aber nicht vorwärts, egal wie stark Du an der Leine ziehst.

Ich würde den Schuhwinkel eigentlich gerne mehr berücksichtigen, so ähnlich wie in der Abbildung vom Skifahren vom DSV in dem Link, hast du die mal angeschaut?

Ich denke, dass ich den Schuhwinkel (die $24°$ ) in meiner Antwort berücksichtigt habe. Wobei ich mir noch nicht sicher bin, ob ich den Winkel bei den Wegen ausreichend berücksichtigt habe ...

Die Bilder des DSV hab ich mir angeschaut, da war jetzt für mich aber nichts neues dabei.

Gruß Werner

Kommentiert 22 Jan 2020 von Werner-Salomon

Ein anderes Problem?

Stell deine Frage

Leistung beim Rollschuh bergauf fahren

2 Antworten

Ähnliche Fragen

Eingabetools:

Beliebte Fragen:

Heiße Lounge-Fragen: