Hallo Mia Katharina,
mache Dir bei sowas immer eine Skizze.
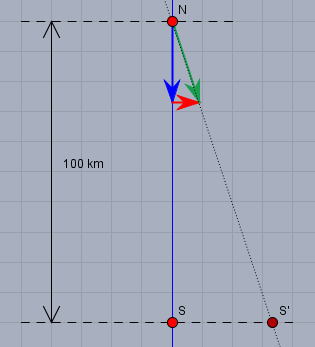
Das Flugzeug startet bei \(N\) und fliegt Richtung Süden, also in der Skizze senkrecht nach unten. Auf unseren üblichen Karten ist Süden i.A. unten. Der blaue Pfeil steht für seine Geschwindigkeit \(v_L\) und Richtung. Gleichzeitig kommt Wind von Westen, also von links, mit der Geschwindigkeit \(v_W\). Dafür steht der rote Pfeil.
Stelle Dir dazu vor, das Flugzeug ist einer riesigen Kiste (der umgebenden Luftmasse). Die Kiste ist geschlossen. Innerhalb der Kiste bewegt sich das Flugzeug nach Süden, aber die Kiste selbst bewegt sich Richtung Osten. Beide Geschwindighkeiten werden sich also aufaddieren und der Weg des Flugzeuges über Grund ist der grüne Pfeil.
Die relative Geschwindigkeit \(v_G\) über Grund kann man über den Pythagoras berechnen. Dazu rechne ich zunächst die m/s in km/h um$$25 \frac{\text{m}}{\text{s}} = 25 \frac{\frac 1{1000} \text{km}}{\frac 1{3600} \text{h}} = 25 \cdot 3,6 \frac{\text{km}}{\text{h}} = 90 \frac{\text{km}}{\text{h}} $$nun in den Pythagoras einsetzen
$$|v_G| = \sqrt{|v_L|^2 + |v_W|^2} = \sqrt{270^2 + 90^2} \frac{\text{km}}{\text{h}} \approx 284,6\frac{\text{km}}{\text{h}} $$
(b) kann man über den Strahlensatz berechnen. Die Länge des rote Pfeil zur Länge des blauen verhält sich genau wie \(|SS'|\) zu \(|NS|\):$$\frac{90}{270} = \frac{|SS'|}{100 \text{km}} \implies |SS'| = \frac 13 \cdot 100 \text{km} \approx 33,3 \text{km} $$man kann das aber auch über die (Flug-)Zeit \(t_F\) berechnen. Das Flugzeug legt in der Luft (nicht über dem Boden, sondern in der 'Kiste') 100km zurück. Dazu benötigt es$$ t_F= \frac{100 \text{km}}{270 \frac{\text{km}}{\text{h}}} = \frac{10}{27} \text{h}$$Der Wind versetzt die Luftmasse (die 'Kiste'), in der sich das Flugzeug befindet in der Zeit \(t_F\) um $$|SS'| = 90 \frac{\text{km}}{\text{h}} \cdot \frac{10}{27} \text{h} = \frac{100}{3} \text{km} \approx 33,3 \text{km}$$
(c) Der Weg \(s_G\) über Grund geht mit Kenntniss von \(|SS'|\) über den Pythagoras $$s_G = \sqrt{100^2 + 33,3^2}\text{km} \approx 105,4 \text{km}$$ oder über die Flugzeit \(t_F\) und die oben berechnete Geschwindigkeit \(v_G\) über Grund$$s_G = |v_G| \cdot t_F = 284,6\frac{\text{km}}{\text{h}} \cdot \frac{10}{27} \text{h} \approx 105,4 \text{km}$$
(d) Um die Richtung zu ermitteln, in die man das Flugzeug steuern muss, um den Südkurs zu halten, beginnt man diesmal beim Ziel. Also beim Punkt \(S\).
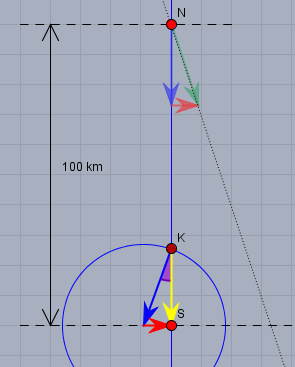
Dort zeichnet man den Windpfeil (rot) ein; und zwar so, dass die Spitze auf \(S\) zeigt. Am Wind kann man nichts ändern! Der Sollkurs (die blaue senkrechte Linie) ist schon da. Auf dieser Linie soll das Flugzeug entlang fliegen. Nun schlägt man von Anfang des Windpfeils einen Kreis dessen Radius der Geschwindigkeit des Flugzeugs entspricht. Der Kreis schneidet die Kurslinie im Punkt \(K\). Die Geschwindigkeit über Grund ist nun der gelbe Pfeil.
Zur Erklärung: das Flugzeug befinde sich bei \(K\) und fliegt 6min (1/10h) in Richtung des blauen Pfeils. Dann legt es 27km zurück. in der gleichen Zeit versetzt der Wind die umgebende Luftmasse (unsere Kiste) um 9km nach rechts, also genau auf den Punkt \(S\).
Beachte bitte, dass die beiden Dreiecke, die hier durch die Pfeile entstehen, nicht gleich sind. Für den Vorhaltewinkel \(\alpha\) (violett) kann man sich nun des Arcussinus bedienen, da die Rechtecke rechtwinklig sind. Es ist$$\sin \alpha = \frac{|v_W|}{|v_L|} \implies \alpha = \arcsin\left( \frac{|v_W|}{|v_L|}\right) = \arcsin\left( \frac 13 \right) \approx 19,5°$$ das entspricht einem Kompasskurs von \(180°+19,5° \approx 199°\).
Das ganze kennt man sowohl in der Luft- als auch in der Seefahrt unter dem Begriff des Strömungs- bzw. Winddreiecks, und gehört zu den Grundlagen der Navigation.
(e) Die Geschwindikeit geht wieder über den Pythagoras, da dies hier ein Sonderfall mit einem rechten WInkel zwischen Sollkurs und Wind ist!$$v_G = \sqrt{|v_L|^2 - |v_W|^2 } = \sqrt{270^2 - 90^2} \frac{\text{km}}{\text{h}} \approx 254,6 \frac{\text{km}}{\text{h}}$$Gruß Werner