Aufgabe:
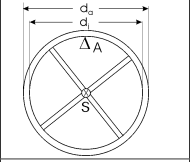
$$ \begin{array}{l}{\text { Physikalisches Pendel: Ein Rad (siehe Abbildung rechts) mit der Masse }} \\ {\mathrm{m}=1 \mathrm{kg}, \text { dem Innendurchmesser } \mathrm{d}_{\mathrm{i}}=96 \mathrm{mm} \text { und dem Außendurchmesser }}\end{array} $$
$$ \begin{array}{l}{ d_{a}=125 \text { mm pendelt an einer Schneide A. Die Perioden- }} \\ {\text { dauer der freien ungedämpften Schwingung beträgt } T_{0}=0,65 \text { s. }} \\ {\text { Berechnen Sie das Massenträgheitsmoment Js bezüglich des }} \\ {\text { Schwerpunkts. }}\end{array} $$
Lösung :$$J_{S}=2,74 * 10^{-3} \mathrm{kgm}^{2}$$
Mein Ansatz wäre mit dieser Formel:
$$ \begin{aligned} \ddot{\beta}+\frac{m g s}{J} \cdot \beta+\frac{b}{J} \cdot \dot{\beta}=0 \end{aligned} $$
wie berechne ich das Massenträgheitsmoment?
$$ \begin{array}{ll}{\text { Vollylinder }} & {J=m R^{2} / 2} \\ {\text { Hohlzylinder }} & {J=m R^{2}, \text { wenn dünne Wände }} \\ {\text { Hohlzylinder }} & {J=m\left(R^{2}+r^{2}\right) / 2, \text { wenn dicke Wände }}\end{array} $$
$$ \begin{array}{ll}{\text { Dünner Stab } J} & {=m l^{2} / 12 \text { (quer durch die Mitte) }} \\ {\text { Dünner Stab } J} & {=m l^{2} / 3 \text { (Rotationsachse am Ende) }} \\ {\text { Kugel }} & {J=2 m R^{2} / 5} \\ {\text { Steiner }} & {J=J_{\text {Schwerpunkt}}+m \cdot s^{2}}\end{array} $$