Physikalisches Pendel: Ein Rad mit der Masse m = 1 kg

Question

Aufgabe:

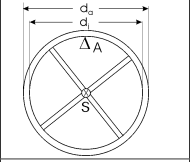
$$\begin{array}{l}{\text { Physikalisches Pendel: Ein Rad (siehe Abbildung rechts) mit der Masse }} \\ {\mathrm{m}=1 \mathrm{kg}, \text { dem Innendurchmesser } \mathrm{d}_{\mathrm{i}}=96 \mathrm{mm} \text { und dem Außendurchmesser }}\end{array}$$

$$\begin{array}{l}{ d_{a}=125 \text { mm pendelt an einer Schneide A. Die Perioden- }} \\ {\text { dauer der freien ungedämpften Schwingung beträgt } T_{0}=0,65 \text { s. }} \\ {\text { Berechnen Sie das Massenträgheitsmoment Js bezüglich des }} \\ {\text { Schwerpunkts. }}\end{array}$$

Lösung :$$J_{S}=2,74 * 10^{-3} \mathrm{kgm}^{2}$$  

Mein Ansatz wäre mit dieser Formel:

$$\begin{aligned} \ddot{\beta}+\frac{m g s}{J} \cdot \beta+\frac{b}{J} \cdot \dot{\beta}=0 \end{aligned}$$

wie berechne ich das Massenträgheitsmoment?

$$\begin{array}{ll}{\text { Vollylinder }} & {J=m R^{2} / 2} \\ {\text { Hohlzylinder }} & {J=m R^{2}, \text { wenn dünne Wände }} \\ {\text { Hohlzylinder }} & {J=m\left(R^{2}+r^{2}\right) / 2, \text { wenn dicke Wände }}\end{array}$$

$$\begin{array}{ll}{\text { Dünner Stab } J} & {=m l^{2} / 12 \text { (quer durch die Mitte) }} \\ {\text { Dünner Stab } J} & {=m l^{2} / 3 \text { (Rotationsachse am Ende) }} \\ {\text { Kugel }} & {J=2 m R^{2} / 5} \\ {\text { Steiner }} & {J=J_{\text {Schwerpunkt}}+m \cdot s^{2}}\end{array}$$

Answer 1

Hallo

(Trägheitsmoment = Differenz der Trägheitsmomente von 2 Vollzylindern. da die Masse und Maße  der Speichen nicht einzeln angegeben ist, wird der Anteil wohl vernachlässigt.wenn du die Formel für Hohlzylinder mit dicken Wänden verwenden darfst, nimm die .)

Allerdings sollst du J und daraus Js wohl nicht aus den Radien ausrechnen sondern aus der Schwingungsdauer!

da keine Reibung angegeben ist, ist in deiner Dgl. b=0 , s=Abstand Schneide - Schwerpunkt, mit der Dgl. ω und damit T bestimmen, daraus J und mit Steiner daraus Js.

Gruß lul

Comments

okay, ich hätte J jetzt mit den Radien berechnet. wie mache ich das denn mit der Schwingungsdauer?

---

 mit den Radien bekommst du nicht das gegebene Ergebnis, da weisst du ja auch nichts über die Speichen.

Du kennst die Lösung der Dgl oder du findest sie, dann hast du die Kreisfrequenz und daraus T und daraus J

Aber eigentlich hatte ich das gesagt.

grüß lul

---

was mache ich falsch?

---

 du setzest Klammern falsch oder nicht.

 rechne erst einfach  J aus ,dann brauchst du keine Klammern , dann daraus Js

---

kannst du mir das mit den Klammern zeigen? ich habe das 100 mal aufgeschrieben.

---

 warum folgst du nicht meine Vorschlag erst j zu berechnen

eine Klammer z B. die fehlt:  4pi²*(Js+ms²) in deiner dritten Zeile

---

danke, habe den Fehler gefunden.