Welche Formel gibt die richtigen Einheit an?

Question

Aufgabe:

Wird eine Flüssigkeit entlang eines Rohres geleitet, dessen Querschnitt nicht immer überall gleich ist, so ändert sich entlang des Rohres der Druck. Die Druckdifferenz Δp, die zwischen zwei Stellen auftritt, hängt von der Fließgeschwindigkeit v1 bzw. v2, die an diesen Stellen herrscht, aber auch von der Dichte p der Flüssigkeit ab.

p wird in kg/m^3, v in m/s und Δp in kg/m*s^2

Nun ist zu prüfen, welcher der aufgeführten Formeln Δp die richtige Einheit zuweist.

Dabei habe ich für p und v immer die Einheit eingesetzt und den Term verrechnet. Doch auf diese Weise eliminieren sich Terme etc. und die für Δp kommt nicht das Gesuchte raus. Warum ist es aber falsch für p und v die Einheit einzusetzen und den Term einfach auszurechnen? (Die Lösung kenne ich bereits und anscheinend müssen nur die Produkte betrachtet werden, aber mit welcher Begründung?)

Hier einmal die Formeln:

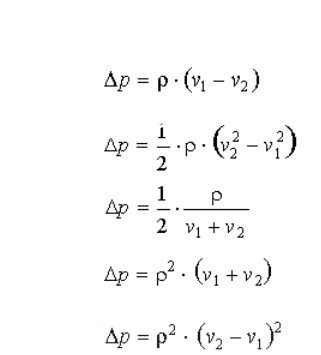
Problem/Ansatz:

Answer 1

Hallo

 Um die Einheit von Δp auszurechnen, kannst du natürlich einfach die Einheiten der einzelnen Teile einsetzen , was du damit meinst, dass sich Terme eliminieren kann ich nur ahnen

 wenn v die Einheit m/s hat,  dann hat natürlich v1-v2 immer noch die Einheit m/s im ersten Fall hast du also als Einheit rechts kg/m^3*m/s im zweiten kg/m^3*m^2/s^2 was die richtige Einheit gibt. wenn du (13€-5€) rechnest hast du nicht die Zahl 8 in der Hand sondern 8€! oder wie geht es dir, wenn du von 13€ 5€ ausgibst?

Gruss lul

Comments

Aber mit eliminieren meine ich das: wenn ich das erste nehme, also p(v1-v2) dann ist das pv1-pv2 und das ist eingesetzt kg/m^3*m/s - kg/m^3*m/s = kg/m^2*s - kg/m^2*s = 0

Deshalb scheint mir die Methode unsinnig, um die korrekte Formel zu bestimmen. Denn wenn man den Term kürzt, kommt 0 raus.

Anscheinend macht es hier nur Sinn, wenn man die Produkte betrachtet, z.B. im oberen Fall dann nur pv1 oder pv2 und dort prüft, ob die Einheit der gesuchten entspricht.

---

 wenn du 2 mit Einheiten behaftete Größen voneinander abziehst, bleibt die Einheit erhalten, das hab ich versucht dir mit den € zu erklären! Sogar wenn die Größen selber verschwinden!  also 5€-5€ sind 0 € und nicht die Zahl 0

 du würdest sagen ich hab keinen Euro mehr,  oder ich hab 0 Euro und nicht ich hab 0, oder ich hab nix, denn du hast ja noch z.b. einen Kopf!

---

Haha super danke! :) Habs jetzt verstanden.