Hallo probe,
Wenn man in der Mechanik eine feste Einspannung frei schneidet, so bedeutet das, dass man die Einspannung durch alle Kräfte ersetzt, die das Lager (also die Einspannung) auf das frei geschnittene Gebilde ausübt. Ein Freischnitt eines Festlagers in 2D ersetzt das Lager durch alle Kräfte und Momente, die in 2D auftreten können. In 3D wären es dann alle in 3D - also drei Koordinatenrichtungen und drei Momente!
Bleiben wir bei bei 2D, so sind es zwei Kräfte in zwei Koordinatenrichtungen und ein Moment. Ich mache mal ein triviales Beispiel:
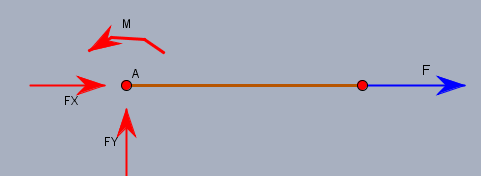
Der braune Balken, sei am Punkt \(A\) fest eingespannt. Schneide ich ihn frei, so ersetze ich das Lager \(A\) durch die Kräfte \(F_x\), \(F_y\) und das Moment \(M\). Und anschließend fordere ich Kräftegleichgewicht, da sich der eingespannte Balken nicht fort bewegt! Daraus folgt dann unmittelbar, dass \(F_x=-F\) und \(F_y\) sowie \(M\) gleich 0 sein müssen.
Die roten Kräfte und Momente sind die Kräfte und Momente, die auf den Balken wirken. Kräfte und Momente auf das Lager \(A\) wirken entsprechend negative zu der angenommenen Richtung.
"Und was zeigen die schwarzen Punkte?" ich bin mit dieser Darstellung nicht vertraut. Ich vermute aber, dass es sich um ein Loslager handelt, dass aber ein Moment aufnehmen kann. Wenn es kein Moment aufnehmen könnte, so wird es (wurde es zu meiner Zeit!) als kleiner Kreis - also nicht ausgefüllt - dargestellt. Das bedeutet, dass dieses Lager keine Kräfte in senkrechter Richtung aufnehmen kann - oben in der Skizze wäre also \(F_y\) dann sicher \(=0\).
Was es genau ist, ist reine Definitionssache!
Ist es ein Loslager, was auch kein Moment aufnehmen kann, wäre auch \(M=0\). Dann bliebe nur \(F_x\) als einzige Lagerkraft übrig.
Gruß Werner