"Wie löse ich solch eine Aufgabe?" immer erst eine Skizze machen:
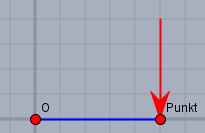
"Heisst F(0/-4N) nicht, dass die Kraft im Ursprung angreift?" Nein - es heißt nur, dass die Kraft einen Betrag von \(4\text{N}\) hat und in negative Y-Richtung wirkt. Die Kraft ist nur als ein Vektor beschrieben, und den kann man zunächst beliebig verschieben - bis
"Nun wirkt die Kraft F (0/-4N) auf diesen Punkt"
zur Angabe, an welcher Stelle diese Kraft wirkt.
Das Moment \(M\) berechnet sich aus Hebelarm mal dem Kraftanteil, der senkrecht zum Hebelarm wirkt. In diesem Fall ist das einfach, da Kraft und Hebelarm bereits senkrecht auf einander stehen.
$$M = 5\text{m} \cdot -4\text{N} = -20 \text{Nm}$$
Das Moment ist negativ, da es in negative Drehrichtung wirkt. Formal besser und auch für den allgemeinen Fall geeignet ist das Kreuzprodukt (siehe Kreuzprodukt Anwendungen) aus Hebelarm \(\vec{r}\) mal Kraft \(\vec{F}\).
$$\vec{M} = \vec{r} \times \vec{F} = \begin{pmatrix} 5\text{m}\\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\ -4\text{N}\end{pmatrix} = -20 \text{Nm}$$
Im 2-dimensionalen Fall ist das Moment kein Vektor, sondern ein einzelner Wert, da alle Momente senkrecht zu der 2D-Ebene stehen müssen.