Hallo StrohUnderdog,
Da hilft oft eine Zeichnung
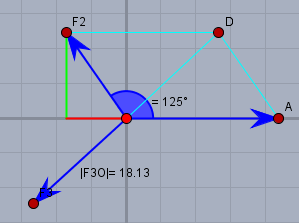
Dein Prof hat wohl recht. Wie rechnet man das? Richtig ist, dass
$$F_3=-(F_1+F_2)$$
Wenn
$$F_1=\begin{pmatrix} 220 \\ 0\end{pmatrix}\text{N}$$
dann ist
$$F_2=\begin{pmatrix} 150 \cdot \cos(125°) \\150 \cdot \sin(125°) \end{pmatrix}\text{N} $$
Beachte, dass \(\cos(125°)<0\) ist (der roteAnteil), während der Sinus (grün) positiv bleibt. Dann erhält man
$$F_3=- \left( \begin{pmatrix} 220 \\ 0\end{pmatrix}\text{N} +\begin{pmatrix} 150 \cdot \cos(125°) \\150 \cdot \sin(125°) \end{pmatrix}\text{N} \right)$$
$$\space \approx \begin{pmatrix} -134,0 \\ -122,9\end{pmatrix}\text{N} \quad \Rightarrow |F_3|\approx 181,78 \text{N}$$
Gruß Werner