Bestimmen Sie die Biegemomente

Question

Aufgabe:

Gegeben ist das folgende statisches System mit zwei einzelasten F₁ und F₂ gemäss Abbildung.

Text erkannt:

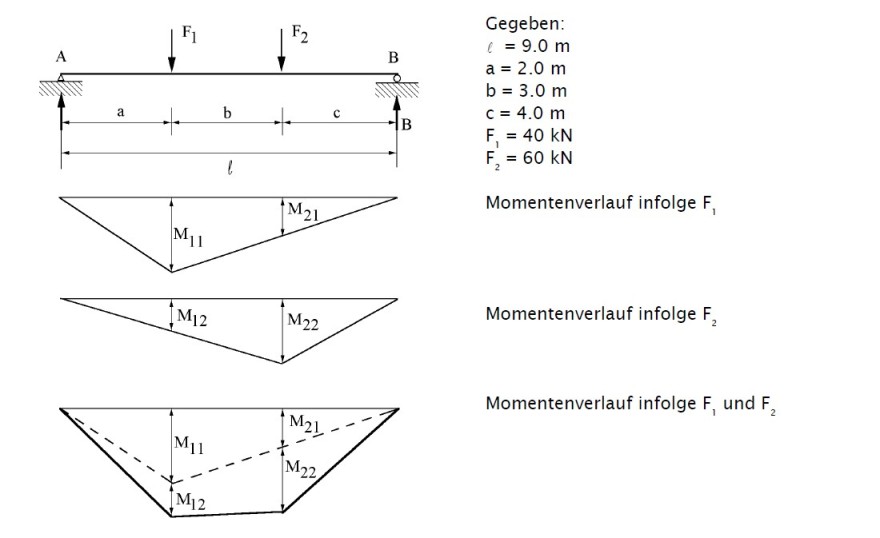
Gegeben:
\( \begin{array}{l} \ell=9.0 \mathrm{~m} \\ \mathrm{a}=2.0 \mathrm{~m} \\ \mathrm{~b}=3.0 \mathrm{~m} \\ \mathrm{c}=4.0 \mathrm{~m} \\ \mathrm{~F}_{1}=40 \mathrm{kN} \\ \mathrm{~F}_{2}=60 \mathrm{kN} \end{array} \)

Momentenverlauf infolge \( F_{1} \)

Momentenverlauf infolge \( F_{2} \)

Momentenverlauf infolge \( F_{1} \) und \( F_{2} \)

Gesucht

Ermitteln sie den Momentenverlauf infolge zwei Einzellasten und berücksichtigen Sie das Prinzip der Superposition. Bestimmen Sie hierzu die Biegemomente:
a. M11 und M21 infolge F1
b. M12 und M22 infolge F1
c. M1 und M2 infolge F1 und F2

Hinweis:
Der Momentenverlauf infolge mehrerer Lasten kann gefunden werden, indem man die Momentenverläufe für jede einzelne Last aufträgt und nachher die Momentenordinaten zum Gesamtverlauf des Momentes addiert: Superpositionsprinzip. Von Einzellasten verursachte Momentenverläufe verlaufen immer polygonal. Unter jeder Einzellast entsteht eine Unstetigkeit, also ein Knick. Es genügt somit, die Momente unter den Einzellasten zu bestimmen.

Ergebnisse*
a) M₁₁ = 62.2 kNm; M₂₁ = 35.5 kNm

b) M₁₂ = 53.2 kNm; M₂₂ = 133.3 kNm

a) M₁ = 115.4 kNm; M₂ = 168.9 kNm (max.)

Problem/Ansatz:

Wenn ich mir die Skizze der Momentverläufe anschaue, ist für mich klar, warum dann in der dritten und letzten Skizze die beiden vorherigen Skizzen „ zusammengerechnet“ werden. Was mir aber nicht klar ist, sind die Ergebnisse. Warum ist M₁₁ 62,2 kNm? Ich habe M am Punkt F1 berechnet und erhalte 179,8 kNm.
M₁₁ = -Av x 2,0 + Bx x 7,0
M₁₁= -57,8 x 2,0 + 42,2 x 7,0
M₁₁ = 179,80 kNm

Offensichtlich sind die Ergebnisse korrekt, aber ich verstehe nicht, wo ich einen Fehler beim Aufstellen der Übung gemacht habe. Vielen Dank im Voraus.

Answer 1

wenn nur die Kraft F₁ betrachtet wird, erhalten wir für B ≈ 8,89 kN.

Das ergibt sich durch das Momentengleichgewicht um den Punkt A

\(F_1\cdot a=B\cdot (a+b+c)\)

eingesetzt und nach B aufgelöst ergibt sich o.g. Wert.

Mit dieser Kraft B und dem Hebel b + c ergibt sich das Moment von M11 ≈ 62,2 kNm bei der Kraft F₁

Answer 2

Warum ist M11 62,2 kNm?

M₁₁ = (F₁ * a * (b + c)) / l = (40 kN * 2 m * (3 m + 4 m)) / 9 m ≈ 62,2 kNm

Ich habe M am Punkt F₁ berechnet und erhalte 179,8 kNm.

Du hast aber nicht beachtet, dass M₁₁ nur ein Teilergebnis der Superposition ist, d.h. du darfst nicht mit den Lagerkräften rechnen, die sich ergeben, wenn der Träger mit F₁ und F₂ belastet ist, sondern nur mit F₁. In diesem Fall ergeben sich aber niedrigere Lagerkräfte, die du aber nicht extra berechnen brauchst.

M₁₁ = B_V * ( b + c )

Mit B_V = F₁ * a / l ergibt sich: M₁₁ = F₁ * a * ( b + c ) / l

M11 = -Av x 2,0 + Bx x 7,0

Wenn du M₁₁ über die Lagerkräfte ausrechnen möchtest, wäre das M₁₁ = A_V * a = 31,1kN * 2 m = 62,2 kNm oder M₁₁ = B_V * (b + c) = 8,89 kN * (3m + 4 m) = 62,2 kNm, aber nicht beides zusammen.

Wieso schreibst du Bx? Aus der Skizze ist doch ersichtlich, dass auch die Lagerkraft bei B senkrecht nach oben wirkt.