Filter in der Elektrotechnik

Question

Aufgabe:

Stimmen meine Rechnungen?

Es geht um Filter in der Elektrotechnik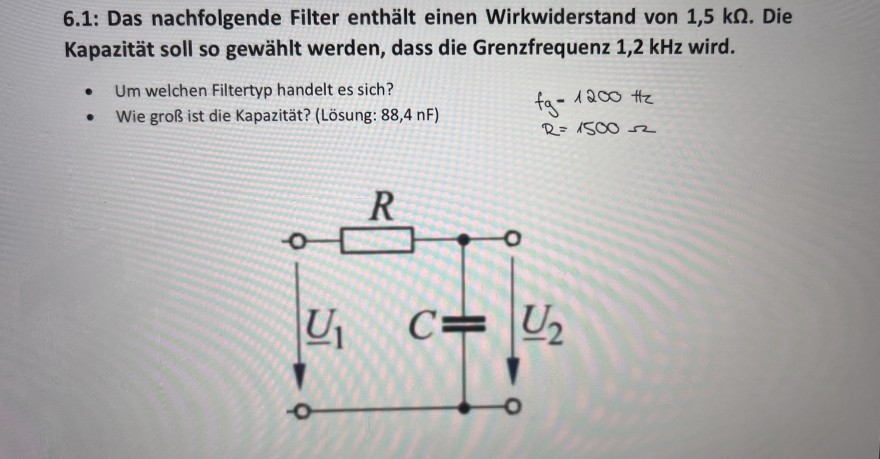

Text erkannt:

6.1: Das nachfolgende Filter enthält einen Wirkwiderstand von 1,5 k \( \Omega \). Die Kapazität soll so gewählt werden, dass die Grenzfrequenz \( 1,2 \mathrm{kHz} \) wird.
- Um welchen Filtertyp handelt es sich?
- Wie groß ist die Kapazität? (Lösung: \( 88,4 \mathrm{nF} \) )
\( \begin{array}{l} \mathrm{fg}-1200 \mathrm{~Hz} \\ R=1500 \Omega \end{array} \)

Text erkannt:

6.2: Gegeben ist ein RL-Tiefpass mit einem ohmschen Widerstand von \( 1,8 \mathrm{k} \Omega \) sowie einer Induktivität von 75 mH .
- Zeichnen Sie die Schaltung
- Wie groß ist das Verhältnis der Ausgangsspannung zur Eingangsspannung bei der Frequenz 15 kHz ?
\( \begin{array}{l} R=1800 \Omega \\ L=75 \mathrm{mH}=0,075 \mathrm{H} \\ f=15000 \mathrm{~Hz} \end{array} \)

Text erkannt:

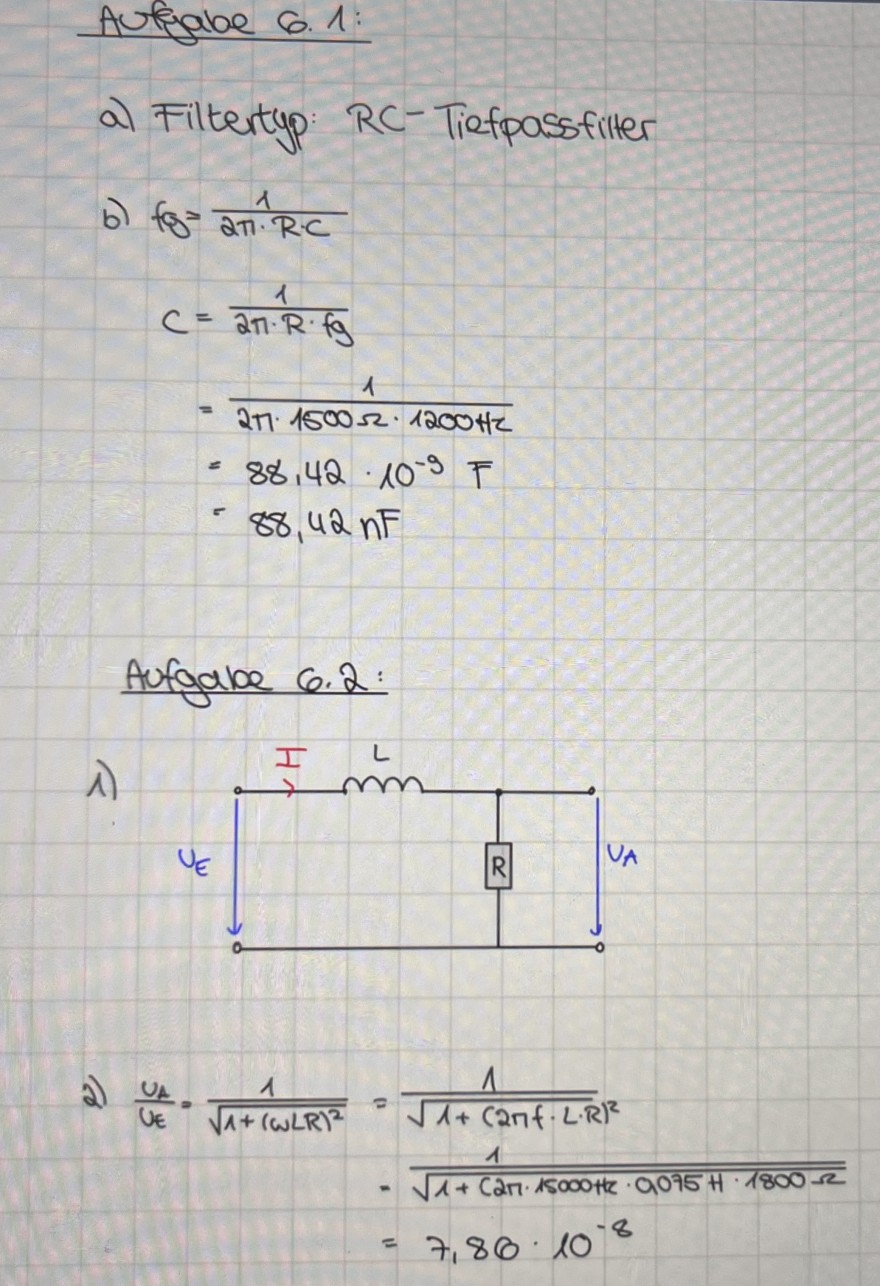
Antrabe 6. 1:
a) Filtertyp: RC-Tiefpassfitter
b) \( f\left(g=\frac{1}{2 \pi \cdot R \cdot C}\right. \)
\( \begin{aligned} C & =\frac{1}{2 \pi \cdot R \cdot f g} \\ & =\frac{1}{2 \pi \cdot 1500 \Omega \cdot 1200 \mathrm{~Hz}} \\ & =88,42 \cdot 10^{-9} \mathrm{~F} \\ & =88,42 \mathrm{nF} \end{aligned} \)

Aufgabe 6.2:
1)
2)
\( \begin{aligned} \frac{U_{A}}{U_{E}} \cdot \frac{1}{\sqrt{1+(\omega L R)^{2}}} & =\frac{1}{\sqrt{1+(2 \pi f \cdot L \cdot R)^{2}}} \\ & =\frac{1}{\sqrt{1+(2 \pi \cdot 15000+k \cdot 0,095 H \cdot 1800 \Omega}} \\ & =7,80 \cdot 10^{-8} \end{aligned} \)

Answer 1

Stimmen meine Rechnungen?

Ob deine Rechnungen richtig sein können, kannst du z.B. vorab selbst überprüfen, indem du feststellst, in welcher Maßeinheit dein Ergebnis herauskommt, wenn du z.B. V/A anstatt Ω, 1/s anstatt Hz und Vs/A anstatt H in deine Formeln einträgst. Bei der 6.1 sieht das dann einheitenmäßig so aus: 1 / (VA^-1 * s^-1) = AsV^-1 = As/V = F. Bei 6.2 kommt gem. deiner Formel einheitenmäßig folgendes heraus: 1 / √(1 + (s^-1 * VsA^-1 * VA^-1)²) = 1 / √(1 + V⁴A^-4). Die 1 als Zahlenwert ohne Einheit kannst du aber nicht zu einem Zahlenwert mit der Einheit V⁴/A⁴ addieren. Außerdem müsste als Ergebnis ein Zahlenwert ohne Einheit herauskommen, weil die Einheit V, die jeweils über und unter dem Bruchstrich steht, eliminiert werden kann. Aber auch dein Zahlenwert ist unrealistisch niedrig, denn der würde ja bedeuten, dass der Spannungsabfall an dem Widerstand verschwindend gering gegenüber dem an der Spule wäre. Folglich müssen deine Formel und dein Ergebnis falsch sein.

Deine Rechnung zu 6.1 ist richtig (Zahlenwert und Maßeinheit).

Zu 6.2 :

U_A / U_E = R / Z = R / √( R² + X_L²) = 1 / (1/R * √(R² + X_L²)) = 1 / √ (1/R² * (R² + X_L²)

 = 1 / √ (1 + (X_L/R)²) = 1 / √ (1 + (2π * f * L / R )²

= 1 / √ (1 + (2π * 15 * 10³ * s^-1 * 75 * 10^-3 VsA^-1 / 1,8 * 10³ VA^-1)² ≈ 0,247

Comments

Text erkannt:

\( \begin{aligned} \frac{U_{A}}{V_{f}} & \left.=\frac{R}{\sqrt{R^{2}+X_{L}^{2}}} \right\rvert\, \frac{1 / R}{1 / R} \\ & =\frac{1}{\sqrt{\left(\frac{1}{1}\right)^{2} \cdot\left[R^{1}+x_{L}^{2}\right]}} \\ & =\frac{1}{\sqrt{1+\left(n x_{L}\right)^{2}}} \\ & =\frac{1}{\sqrt{7+(\omega L R)^{2}}}\end{aligned} \)

Mein Prof hat folgendes gerechnet. Die Rechnung unterscheidet sich zu ihrer. Deshalb kommt bei mir auch etwas anderes raus. Ist seine Rechnung also falsch?

---

Nachdem was ich dir geschrieben habe, solltest du eigentlich in der Lage sein, festzustellen, welche Rechnung richtig ist, welche falsch oder ob beide falsch sind, so dass du nicht mir oder deinem Prof einfach nur glauben musst. Ist dir denn bei beiden Rechnungen alles klar? Auch wenn du nicht alle Rechenschritte nachvollziehen kannst, dann überprüfe doch wenigstens anhand der jeweils letzten Gleichungen, welche Einheiten bei beiden Rechnungen herauskommen.

Unter der Wurzel steht doch bei dir bzw. deinem Prof und mir :

(1 / R) ² * (R² + X_L²).

Soweit sind wir ja uns noch einig.

Wenn ich das ausmultipliziere erhalte ich aber:

R² / R² + X_L² / R²  = 1 + (XL / R) ² und nicht   1 + (R * X_L)².

Ich nehme an, dass du diese einfache Rechnung nachvollziehen kannst und dann selbst entscheiden, was von beidem richtig ist.