Aufgabe:
Text erkannt:
3.4:
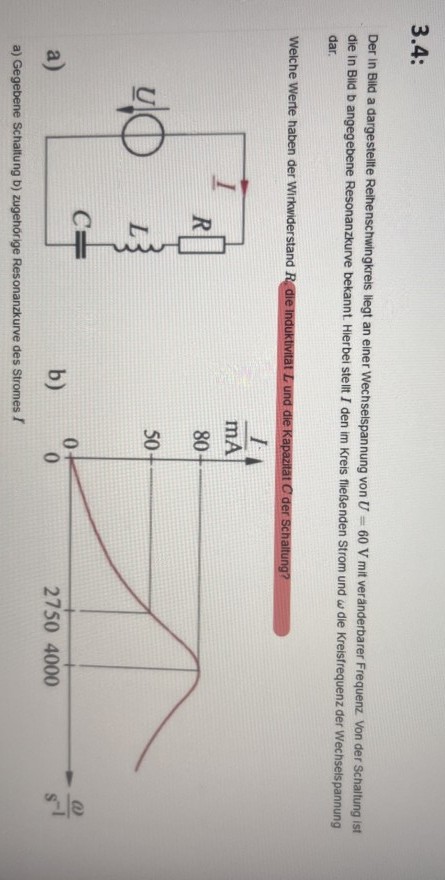
Der in Bild a dargestellte Reihenschwingkreis liegt an einer Wechselspannung von \( U=60 \mathrm{~V} \) mit veränderbarer Frequenz. Von der Schaltung ist die in Bild b angegebene Resonanzkurve bekannt. Hierbei stellt \( I \) den im Kreis fließenden Strom und \( \omega \) die Kreisfrequenz der Wechselspannung dar.
Welche Werte haben der Wirkwiderstand \( R \) die Induktivitat \( L \) und die Kapazitat \( C \) der schaltung?
a)
b)
a) Gegebene Schaltung D) zugehörige Resonanzkurve des Stromes \( I \)

Text erkannt:
Aurgabe 3.4
\( I R=80 \mathrm{~mA}=0,08 A \quad \) Resonanz: \( x_{L}=\omega L \) und \( x_{c}=\frac{1}{\omega c} \)
\( \omega R=4000 \mathrm{sen}^{-1} \)
Berechnung des Widerstands
a) \( R-\frac{1}{I_{\text {Hax }}}=\frac{60 \mathrm{~V}}{80 \cdot 10^{-3} \mathrm{~A}}=750 \Omega \)
Berechnung der Impedanz z (Gesamtwiderstand):
bei \( \omega_{1}=2750 \mathrm{~s}^{-1} \) fließt \( I_{1}=50 \mathrm{~mA}=50 \cdot 10^{-3} \mathrm{~A} \) dabei: \( z_{1}=\frac{u}{I_{1}} \cdot \frac{60 v}{50.10^{-3} \lambda} \cdot 1200 \Omega \)
bei WA gitt:
\( u^{2}=R^{2}+\left(w_{x} L-\frac{1}{w_{x} \cdot c}\right)^{2} \)
Weiterhin gitt bei Resonanz (WR \( =4000 \operatorname{sek}^{-1} \) )
LR. \( L-\frac{1}{\text { WR.C }} \rightarrow \) nach \( C \) autlossen
\( C=\frac{1}{\omega R^{2} \cdot L} \)
wir mochten \( \hat{\text { whe }} \)
\( \begin{array}{l} \frac{1}{\omega_{1} c}=\frac{1}{\omega x c} \quad k c= \end{array} \)
\( \begin{array}{l} =\frac{1}{W_{1} C}=\frac{U R^{2}}{L d} \cdot L \\ \text { Eingesetet in } z_{1}^{2} \end{array} \)
Folgende Rechnung habe ich bisher. Der Wert von L= stimmt auch an sich, allerdings ist das Vorzeichen falsch. Wo liegt mein Fehler?