meine Vorgehensweise: Unterteilung in drei Teilsysteme
Jedes Teilsystem wird "freigeschnitten", d.h., die Umgebung wird weggenommen und dafür Kräfte angesetzt. Mit FS habe ich die Seilkräfte bezeichnet. Da wir hier ein beschleunigtes System haben, kommen die Trägheitskräfte noch hinzu.
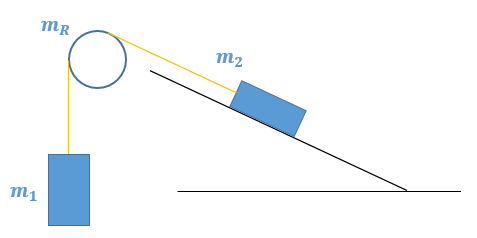
Für m1 gilt
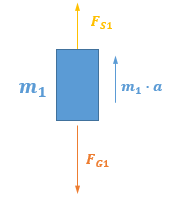
Für die Rolle mit mR gilt:
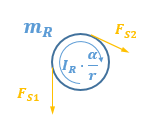
FS2 ist kleiner als FS1 weil die träge Rolle in Rotation versetzt wird.
Und für m2 gilt:
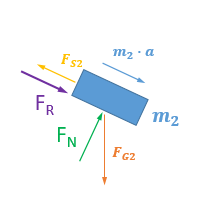
die Hangabtriebskraft, wie sie anfangs bei schiefen Ebenen eingezeichnet wurde, erscheint hier nicht. Beachte die Richtung von FR, der Untergrund drückt in diese Richtung gegen m2.