Aufgabe:
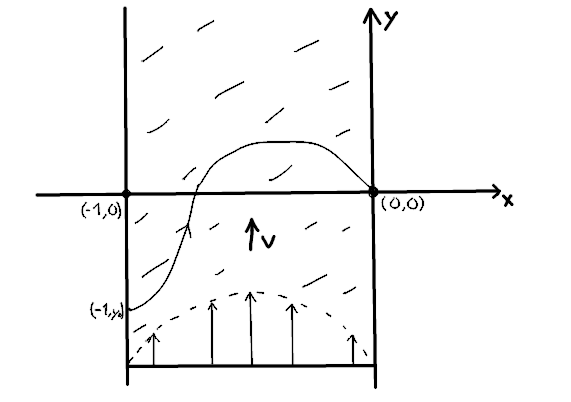
Ein Hund durchschwimmt einen Fluss der Breite 1 mit konstanter Eigengeschwindigkeit 1 relativ zum Wasser so, dass seine Schnauze stets auf sein Herrchen gerichtet ist, welches ortsfest im Punkt (0,0) am gegenüberliegenden Ufer steht. Der Hund starte im Punkt (-1, y0), wobei y0 ∈ ℝ beliebig sei (s. Skizze).
Die Geschwindigkeitsverteilung der Strömung in Abhängigkeit von der Strecke entlang der x-Achse (s. Skizze) sei mit der Funktion v(x) = -2x(1+x), -1 ≤ x ≤ 0 angegeben. Es sei y: [-1, 0] → ℝ die eindeutig bestimmte Funktion mit der Eigenschaft, dass Graph(y) = {(x,y(x)): x ∈ [-1, 0]} eine Umparametisierung des Weges ist, den der Hund schwimmt. Man stelle eine Differentialgleichung für y(x) auf und löse diese.
Problem/Ansatz:
Mein Ansatz wäre, die Bewegung des Hundes zunächst in x- und y-Richtung aufzuteilen. Weil seine Schnauze immer zum Koordinatenursprung zeigt, ist der Winkel zwischen seiner Längsachse und der x-Achse abhängig von seiner Position, also α = arctan(y/x). Dann kann man für die Bewegung in x-Richtung angeben
$$\frac{dx}{dt} = cos(arctan\left(\frac{y}{x}\right)) = \frac{1}{\sqrt{1 + (\frac{y}{x})^2}}$$
und für die Bewegung in y-Richtung
$$\frac{dy}{dt} = sin(arctan\left(\frac{y}{x}\right)) -2x(1+x) = \frac{\frac{y}{x}}{\sqrt{1 + (\frac{y}{x})^2}} -2x(1+x)$$
Dann kann man schreiben
$$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = -2x(1+x)\sqrt{1 + \left(\frac{y}{x}\right)^2} + \frac{y}{x}$$.
Dies ist eine Differentialgleichung für y(x). In der Vorlesung (Einführung in die theoretische Physik) habe ich noch den Hinweis erhalten, die Gleichung durch Substitution mit z = (y/x) zu vereinfachen. Doch das genaue Vorgehen bei der Lösung erschließt sich mir daraus nicht, weil ich am Ende eine implizite Gleichung erhalte, die auch nach Trennung der Variablen und beidseitiger Integration nicht einfach nach z umzuformen ist. Ich komme durch oben genanntes Vorgehen auf den Ausdruck
$$\sqrt{z^2 + 1} + z = Ce^{-2x-x^2}$$
Vielleicht kann hier ja jemand helfen und meinen Ansatz überprüfen.