Aufgabe:
Eine Wärmekraftmaschine durchläuft den folgenden Kreisprozess und ist durch ein ideales Gas betrieben:
1. Isotherme Kompression bei der Temperatur T1,
2. Isochore Erwärmung bei einem Volumen V1,
3. Isotherme Expansion bei der Temperatur T2,
4. Isochore Abkühlung bei einem Volumen V2.
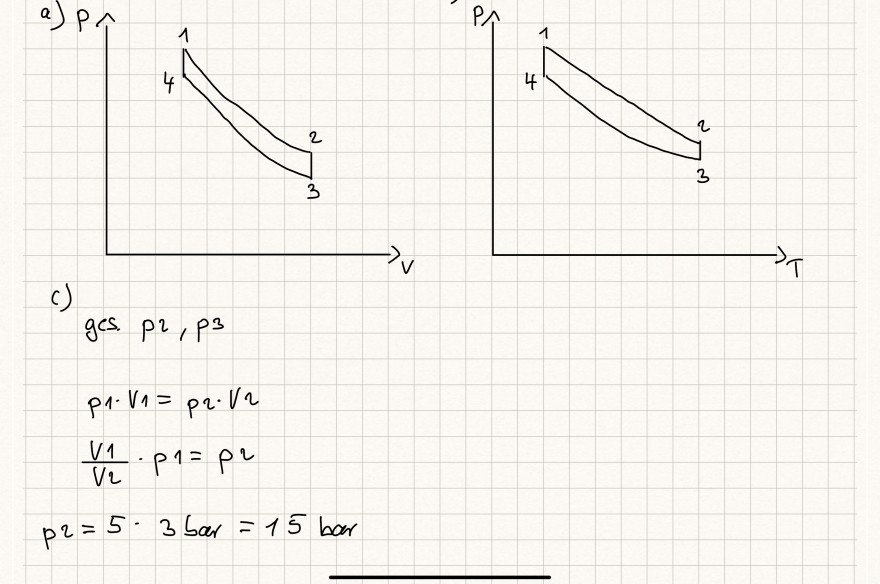
(a) Zeichen Sie das pV-Diagramm des Kreisprozesses;
(b) Zeichen Sie das \( p T \)-Diagramm des Kreisprozesses;
(c) Berechnen Sie \( p_{2} \) und \( p_{3} \).
Gegeben: \( p_{1}=3 \) bar \( p_{4}=20 \) bar \( \frac{V_{1}}{V_{2}}=5 \)
Problem/Ansatz:
Text erkannt:
a)
c)
ges. \( p^{2}, p^{3} \)
\( \begin{array}{c} p_{1} \cdot V_{1}=p_{2} \cdot V_{2} \\ \frac{V_{1}}{V_{2}} \cdot p_{1}=p_{2} \\ p_{2}=5 \cdot 3 \text { bar }=15 \text { bar } \end{array} \)
Guten Morgen, die Aufgabe b bekomme ich leider nicht gelöst. Kann mir da jemand weiterhelfen?
Zudem die Grafischen Darstellungen. Stimmen die so?
Viele Grüße und schonmal vielen Dank.