Berechnen Sie die Mindestmasse von m 2 , damit m 1 nicht nach unten abrutscht..

Question

Text erkannt:

6. Gegeben sei folgende Situation (siehe Skizze) mit \( m 1=1 \mathrm{~kg} \varphi=45^{\circ} \quad \mu_{\mathrm{H}}=0,462 \) Die Seile seien masselos und die Umlenkrolle reibungsfrei. g sei \( 10 \mathrm{~m} / \mathrm{s}^{2} \) Runden Sie alle Berechnungen auf 2 Stellen nach dem Komma.
a) Berechnen Sie die Mindestmasse von \( m 2 \), damit \( m 1 \) nicht nach unten abrutscht..
b) Berechnen Sie die Mindestmasse von \( \mathrm{m} 2 \), damit \( \mathrm{m} 1 \) nach oben gezogen wird.
c) Wenn \( m 2=0 \) wäre, bis zu welchem Winkel \( \varphi \) würde \( m 1 \) noch nicht nach unten abrutschen?

Aufgabe:

Answer 1

ich erkläre 'mal a)

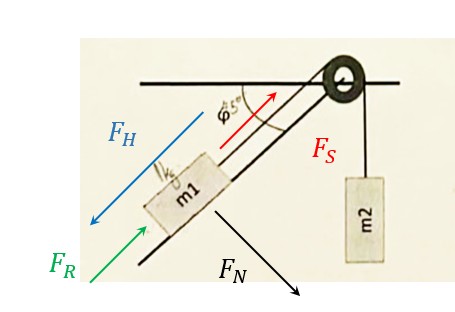
wenn m₁ nach unten rutscht, dann wirkt die Reibkraft F_R gegen die Bewegungsrichtung an der Masse. Die Normalkraft F_N ist Gewichtskraft F_G1·cos(φ). Die Reibkraft F_R ist F_N·μ ; die Hangabtriebskraft F_H ist F_G·sin(φ).

F_S und F_R müssen = F_H sein, damit m₁ gerade nicht nach unten rutscht. Aus der Seilkraft läßt sich m₂ berechnen.

Kommst du damit weiter, ansonsten bitte melden.