Statistische Auswertung (Fadenpendel) / Vergleich Verteilungsdichten

Question

Text erkannt:

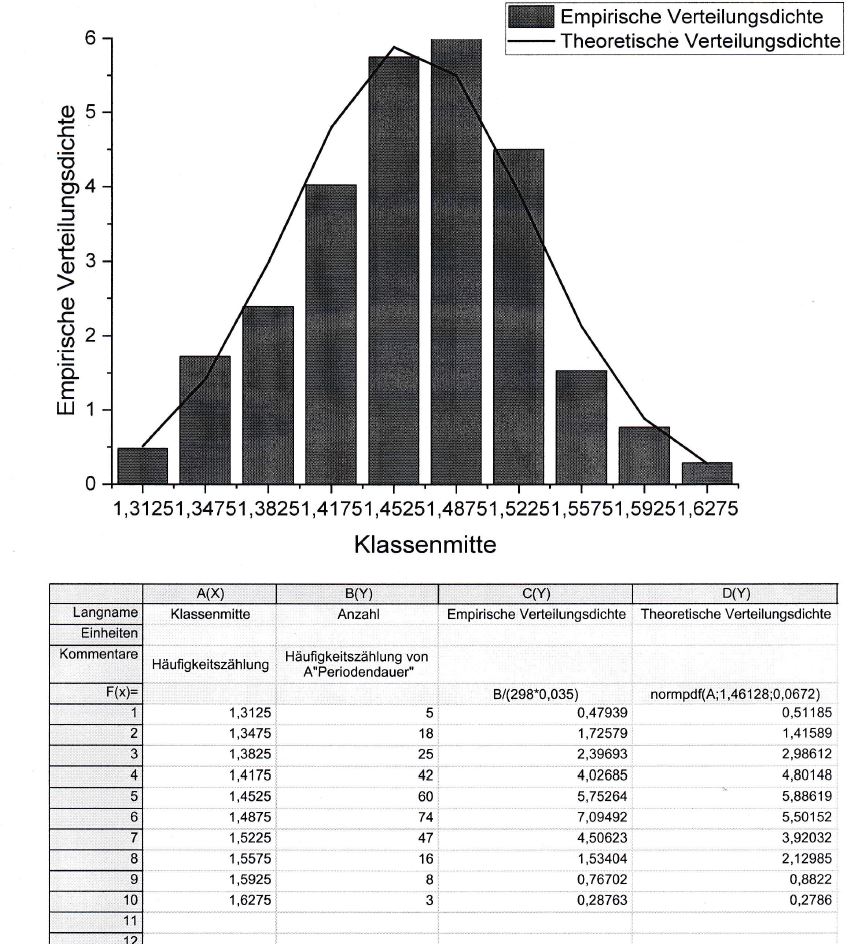
Klassenmitte
\begin{tabular}{|c|c|c|c|c|}
\hline & \( A(X) \) & \( B(Y) \) & \( \mathrm{C}(\mathrm{Y}) \) & \( D(Y) \) \\
\hline Langname & Klassenmitte & Anzahl & Empirische Verteilungsdichte & Theoretische Verteilungsdichte \\
\hline \multicolumn{5}{|l|}{ Einheiten } \\
\hline Kommentare & Häufigkeitszählung & \begin{tabular}{l}
Häufigkeitszählung von \\
A"Periodendauer"
\end{tabular} & & \\
\hline\( F(x)= \) & & & \( B /\left(298^{\star} 0,035\right) \) & normpdf(A;1,46128;0,0672) \\
\hline 1 & 1,3125 & 5 & 0,47939 & 0,51185 \\
\hline 2 & 1,3475 & 18 & 1,72579 & 1,41589 \\
\hline 3 & 1,3825 & 25 & 2,39693 & 2,98612 \\
\hline 4 & 1,4175 & 42 & 4,02685 & 4,80148 \\
\hline 5 & 1,4525 & 60 & 5,75264 & 5,88619 \\
\hline 6 & 1,4875 & 74 & 7,09492 & 5,50152 \\
\hline 7 & 1,5225 & 47 & 4,50623 & 3,92032 \\
\hline 8 & 1,5575 & 16 & 1,53404 & 2,12985 \\
\hline 9 & 1,5925 & 8 & 0,76702 & 0,8822 \\
\hline 10 & 1,6275 & 3 & 0,28763 & 0,2786 \\
\hline 11 & & & & \\
\hline
\end{tabular}

Aufgabe:

Hallo liebes Forum. Wir hatten die Aufgabe mittels (Experiment) Fadenpendel die Fallbeschleunigung zu errechnen. Ist aber jetzt nicht entscheidend!

Der Teil um den es geht, war das wir mittels unserer 298 Durchführungen ein Darstellung aus Säulendiagramm(empirische Verteilungsdichte) und Gaußsche Glockenkurve(theoretische Verteilungsdichte) erstellen sollen.

Nun sollten Wir mittels Standardabweichung s = 0,06248 die Intervalle T-s ≤ T ≤ T+s, also 1,3988 ≤ T ≤ 1,523 festlegen und in % bestimmen wieviele Werte in diesem Intervall liegen für T ± s bin ich dann auf ca. 74% gekommen, was eigentlich nicht sein darf, weil ja die Literatur 68,3% vorgibt. Ebenso für T ± 2s, also 1,33632 ≤ T ≤ 1,58624 mit 95,63%, was eigentlich sehr gut ist, da es nahe dem Literaturwert 95,5% liegt.

Aufgabe:

Vergleichen Sie beide Verteilungsdichten miteinander.

Vergleichen Sie die Ergebnisse mit den Erwartungswerten für normalverteilte Messwerte. (Also warum die % von den Literaturwerten abweichen?)

Problem/Ansatz:

Ich habe leider keine Vorstellung davon, was die Gründe sein könnten, da ich das erste mal darin ein Protokoll schriebe. Ich könnte mir nur Vorstellen, dass die Werte der empirischen Verteilungsdichte über der Gaußschen Glockenkurve liegen und somit eine größere Häufung in den Intervallen erfolgt und somit die 74% zu begründen sind. Wie ich dann die guten 95,63% begründe weiss ich leider nicht. Allgemein weiss ich leider nicht wie man das schön mathematisch begründet und würde mich sehr über eure Hilfe freuen.

Comments

Auf den ersten Blick sehe ich da einen Fehler in der Tabelle.

Statt 7,09492 müsste es wohl 6,09492 heißen?

So ganz verstehe ich deine Frage nicht, aber es ist ja klar, dass bei engerem s auch der Fehler größer sein wird.

---

Statt 7,09492 müsste es wohl 6,09492 heißen?

Wie kommst du darauf? 74/(298*0,035) ≈ 7,09492

---

Es stimmt nicht mit der Grafik überein.

(und wäre auch ein ziemlicher Ausreißer.)

---

Vielen Dank für deine Antwort. Die Unstimmigkeit der Tabellenwerte mit der Grafik war mir noch gar nicht aufgefallen. Weil aber die 7,09492 mittels Formel aus der Häufigkeit rechnerisch richtig ermittelt wurde, müssten die 74 falsch sein. 6,09492 könnte auch nicht sein, weil dann eine nicht ganzzahlige Häufigkeit heraus käme.

Answer 1

Hallo,

ich bin bei den von dir angegebenen Messwerten zu etwas anderen Ergebnissen gekommen: T = 1,4639, s = 0,0629.

Die ändern aber nichts an der Anzahl der Werte, die in den entsprechenden Intervallen liegen, so dass ich auf ca. 74,8% und ca. 94,6% komme. Die Prozentzahlen sollten also eigentlich übereinstimmen.

Die Abweichungen zu den in der Literatur angegebenen Werten könnte z.B. an der relativ geringen Anzahl an Messwerten und/oder an Messfehlern liegen.

Oder es könnte auch ein Ausreißer ursächlich sein (s. Kommentar von willyengland ): Bei der empirischen Verteildichte weicht der Wert von 7,09492 erheblich von dem theoretischen Wert von 5,50152 ab. Weil dieser Wert mittels Formel rechnerisch richtig aus der Häufigkeit ermittelt wurde, könnten die 74 falsch sein. Wenn es z.B. nur 64 gewesen sein sollten, ergeben sich nur noch ca. 71,5% anstatt ca. 74,8%.

Dass bei einem größeren Intervall die Abweichung kleiner ist, als bei einem kleineren Intervall, liegt an der unterschiedlichen Anzahl erfasster Messwerte, sowie der unterschiedlichen Anzahl der Häufigkeit.

In dem Intervall von ± s um den Erwartungswert liegen 4 unterschiedliche Messwerte bei insgesamt 223 Messungen. Die obere Intervallgrenze liegt nur 1,523-1,5225=0,0005 über dem 4. Wert. Fiele der z.B. wegen systematischer, zufälliger und/oder fahrlässiger Fehler weg, würden anstatt ca. 75% nur noch ca. 59% herauskommen.

In dem Intervall von ± 2s um den Erwartungswert liegen aber 7 unterschiedliche Messwerte bei insgesamt 282 Messungen. Fiele da z.B. der 7. Wert weg, würden ca. 89,3% anstatt der ca. 94,6% herauskommen. Die Differenz ist also einmal 16% und das andere Mal aber nur 5,3%.