Aufgabe:
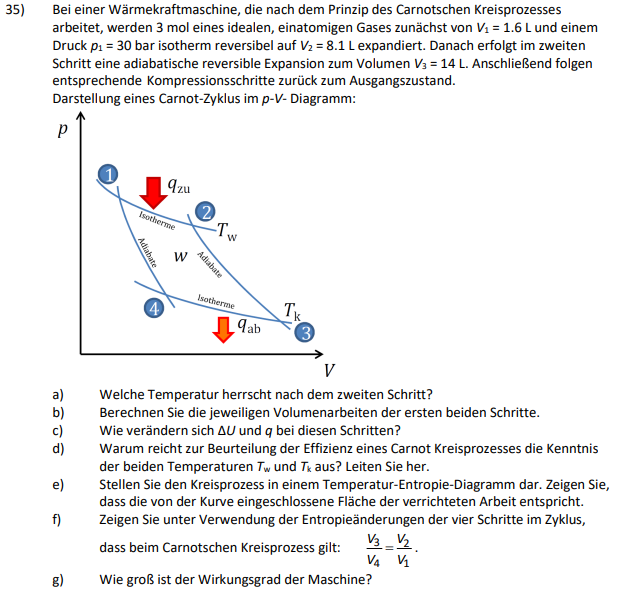
Text erkannt:
35) Bei einer Wärmekraftmaschine, die nach dem Prinzip des Carnotschen Kreisprozesses arbeitet, werden \( 3 \mathrm{~mol} \) eines idealen, einatomigen Gases zunächst von \( V_{1}=1.6 \mathrm{~L} \) und einem Druck \( p_{1}=30 \) bar isotherm reversibel auf \( V_{2}=8.1 \mathrm{~L} \) expandiert. Danach erfolgt im zweiten Schritt eine adiabatische reversible Expansion zum Volumen \( V_{3}=14 \mathrm{~L} \). Anschließend folgen entsprechende Kompressionsschritte zurück zum Ausgangszustand. Darstellung eines Carnot-Zyklus im \( p \) - \( V \) - Diagramm:
a) Welche Temperatur herrscht nach dem zweiten Schritt?
b) Berechnen Sie die jeweiligen Volumenarbeiten der ersten beiden Schritte.
c) Wie verändern sich \( \Delta U \) und \( q \) bei diesen Schritten?
d) Warum reicht zur Beurteilung der Effizienz eines Carnot Kreisprozesses die Kenntnis der beiden Temperaturen \( T_{\mathrm{w}} \) und \( T_{\mathrm{k}} \) aus? Leiten Sie her.
e) Stellen Sie den Kreisprozess in einem Temperatur-Entropie-Diagramm dar. Zeigen Sie, dass die von der Kurve eingeschlossene Fläche der verrichteten Arbeit entspricht.
f) Zeigen Sie unter Verwendung der Entropieänderungen der vier Schritte im Zyklus, dass beim Carnotschen Kreisprozess gilt: \( \quad \frac{V_{3}}{V_{4}}=\frac{V_{2}}{V_{1}} \).
g) Wie groß ist der Wirkungsgrad der Maschine?
Problem/Ansatz:
Mein Problem bei dieser aufgabe ist, dass ich nicht die entsprechenden Lösungen rausbekomme.
Für a) sollen 133.6 K rausbekommen, ich habe allerdings 138.6K
b) schaffe ich es nciht die zweite Volumenarbeit also W(2,3) zu berechnen. Die Formel sollte eigentelich W=Cv*delta T lauten, allerdings komme ich hier nciht auf das richtige Ergebnis.
Für Tipps bei den restlichen aufgaben wäre ich ebenfalls dankbar
MfG