Aufgabe:
Die obere Isotherme mit T1=500K des Carnotprozesses eines idealen Gases (k=1,4) verläuft zwischen den Zuständen
p1= 0,8 MPa V1=2m^3 P2=0,4Mpa V2=4m^3
Wie groß ist P3 und V3, wenn T2= 350K ?
Problem/Ansatz:
Text erkannt:
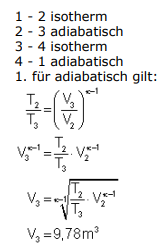
1 - 2 isotherm
\( 2-3 \) adiabatisch
\( 3-4 \) isotherm
4 - 1 adiabatisch
1. für adiabatisch gilt:
\( \frac{T_{2}}{T_{3}}=\left(\frac{V_{3}}{V_{2}}\right)^{k-1} \)
\( V_{3}^{k-1}=\frac{T_{2}}{T_{3}} \cdot V_{2}^{k-1} \)
\( V_{3}=k-1 \frac{\sqrt{T_{2}}}{T_{3}} \cdot V_{2}^{k-1} \)
\( V_{3}=9,78 m^{3} \)
Das steht in der Musterlösung. Ich möchte aber gerne wissen, wie man auf diese Formel kommt, da die in keiner Formelsammlung steht.
Vielleicht kann mir jemand bei meinem Problem weiterhelfen.