Aufgabe:
Hallo, bei A1 habe ich Aufgabe a-c schon gemacht, ich denke Mal das seht ihr schon in den Fotos, ich weiß nur noch nicht ganz was ich bei d machen muss und bei A2, bitte erklärt mir was ich da machen muss
Bei A2 ist hauptsächlich das Problem, ich weiß nicht was es und eb sind und wie man das beschreibt und dann bei b wie ich an die Formel komme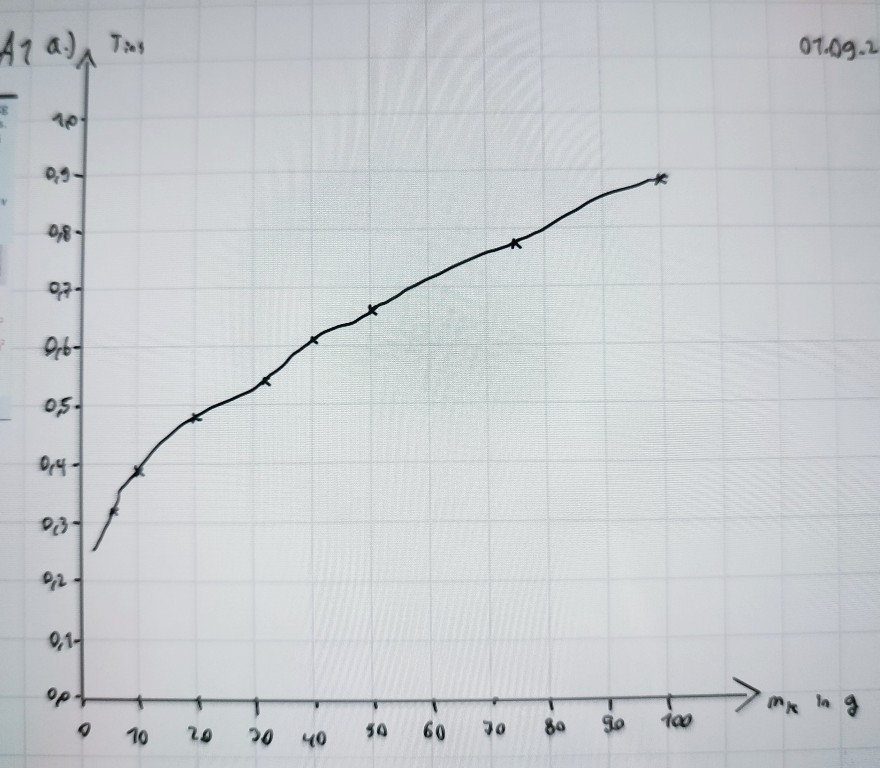

Text erkannt:
b.)
geg:: \( m_{F}=32 g, 032,0=5,54 \frac{\mathrm{N}}{\mathrm{m}} \)
gs: \( T \)
his. \( T=2 \pi \sqrt{\frac{m}{0}} \)
Or.: \( T=2 \pi \sqrt{\frac{0,032}{5,54}} \approx 0,485 \)


Text erkannt:
ges: \( \uparrow \)
losis: \( T=2 \pi \sqrt{\frac{m}{0}} \)
c.)
Dar.: \( T=2 \pi \sqrt{\frac{0,012}{5,54}} \approx 0,48 \) s
\( \begin{array}{l} T=2 \pi \sqrt{\frac{m_{k}+}{0}} \\ T^{2}=4 \pi^{2} \cdot \frac{m_{k+k} \cdot}{D} \\ T^{2} \cdot 0=40^{2} \cdot m_{k+k \cdot m_{k}} \end{array} \)
d.)
\( \frac{T^{2} \cdot 0}{4 \pi^{2}}=m_{k}+x+ \)
Eg: \( K, D=3,54 \frac{2}{m}, 1, k \)
\( \left(\frac{t^{2} \cdot D}{40^{2}}-a x d: a_{F}=k\right. \)
Ss.: \( T_{\text {nore }} \)
hia: \( T_{\text {trore }}=2 \pi \sqrt{\frac{m_{k}+k}{D}} \)
\( 2 \pi \sqrt{\frac{m_{k}+k-m_{F}}{D}} \)
Text erkannt:
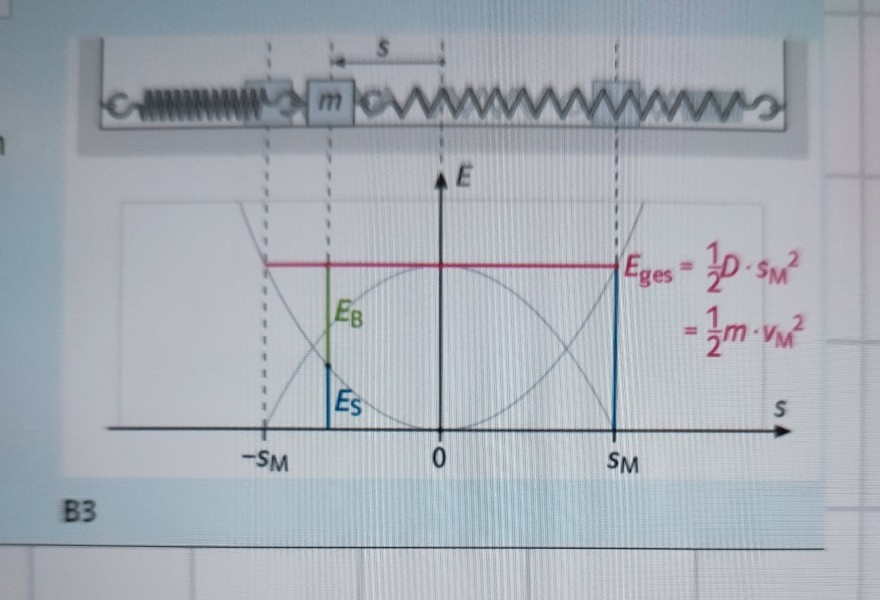
B3
A1 An einer Feder mit der Masse mf=32g und der Federkonstanten D=5,54 N/m schwingt ein Körper mit der Masse mk vertikal. Für Körper mit verschiedener Masse wird die Dauer der Periode T bestimmt:
a) Zeichnen Sie ein mk T-Diagramm.
b) Berechnen Sie T unter Vernachlässigung von mf, und tragen Sie die Werte in das mk T-Diagramm ein. Vergleichen Sie.
c) Berechnen Sie für alle Messwerte den Korrekturfaktor k, der die Masse der Feder in der Formel T= 2 Pi Wurzel aus m/D mit m=mk+k×mf berücksichtigt.
d) Berechnen Sie die Periodendauer Torr unter Verwendung der korrigierten Masse m.
A2 Ein Federpendel der Masse m=0,2kg
schwingt vertikal mit am=8cm und T=1,4s.
a) B3 beschreibt die Energieüberführung bei der Schwingung. Deuten Sie den Verlauf der Komponenten Es, Eb und Eges
b) Bestimmen Sie Es, Eb und Eges für die Zeit- punkte t = T/2 und t = T/8. Bestimmen Sie s, v und a für die Zeitpunkte 0,35s/0,7s/1,0s.