Hallo Christiank,
bevor ich auf die Lösung der Aufgabe eingehe, hier ein paar wichtige Tipps wie man bei der Berechnung von OP- Schaltungen vorgeht:
Zu allererst musst du alle OP-Grundschaltungen gelernt haben und sofort, also auf den ersten Blick erkennen um welche Grundschaltung es sich bei dem OP handelt. Das ist eine absolute Voraussetzung und mit sehr viel Fleiß verbunden. Außer dem sofortigen Erkennen der Grundschaltung musst du die dazugehörigen Gleichungen parat haben.
Es reicht nicht aus die Grundschaltungen mit den dazugehörigen Gleichungen zu kennen, sondern du musst sie beherrschen!
Hier die wichtigsten OP-Grundschaltungen, die du unbedingt erlernen musst:
• Invertierende Verstärkerschaltung
• Nichtinvertierende Verstärkerschaltung
• Addier- und Subtrahierschaltung
• Integrierer
• Differenzierer
• Multiplizierer
• Schmitt-Trigger
Das sind die wichtigsten OP-Grundschaltungen, die du sofort (ohne Nachzudenken) erkennen musst.
Wenn du diese "Ochsentour" hinter dich gebracht hast, dann solltest du keine Probleme mehr mit OP-Schaltungen haben.
Nun zu deiner Aufgabe:
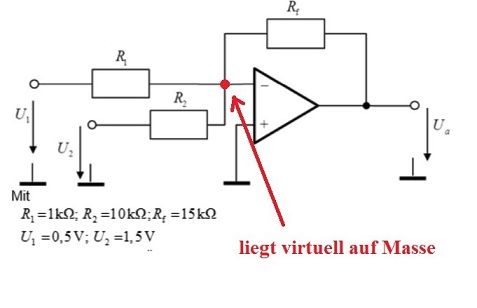
Bei dieser Schaltung handelt es sich einen Addierer, genauer gesagt um einen Umkehraddierer, da invertierend.
Am invertierenden Eingang des OP lässt sich folgende Knotenpunktgleichung aufstellen, da dieser Punkt virtuell auf Masse liegt, siehe Bild.
\(\large \frac{U_{1}}{R_{1}} + \frac{U_{2}}{R_{2}} + \frac{U_{a}}{R_{f}} = 0\)
Stellt man diese Gleichung nach \(\large U_{a}\) um, erhält man:
\(\large U_{a} = - \frac{R_{f}}{R_{1}} * U_{1} - \frac{R_{f}}{R_{2}} * U_{2}\)
Setzt man die Werte ein, so erhält man für \(\large U_{a}\) :
\(\large U_{a} = - 9,75V\)
Gruß von hightech