Ich hoffe, dass dir diese Skizze
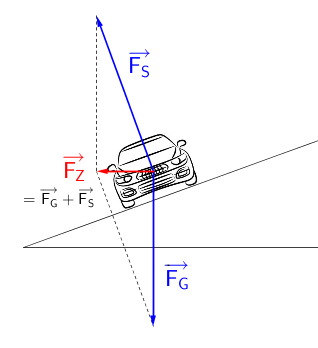
meinen Text erklären kann.
Falls die Straße nicht überhöht ist, sind FS und FG entgegengesetzt gleich, ihre Resultierende ist 0 und gemäß F=m·a findet keine Beschleunigung statt. In diesem Fall müsste die Reibung zwischen Reifen und Straßenbelag die erforderliche Zentripetalkraft für eine Kurvenfahrt aufbringen.
Hier wird die Überhöhung aus der Forderung FR=0 berechnet und damit wird die Gesamtkraft FZ = FG+FS (vektoriell) diejenige Kraft, die gemäß FGes = m·az für die Zentripetalbeschleunigung der Kurvenfahrt aufkommt. Bei deiner Zerlegung wird doch FG=FZ+FS die Gesamtkraft, aber in Richtung von FG findet keine Beschleunigung statt.
Außerdem : Im Fragetext heißt es einerseits Zentrifugalkraft ausgeschaltet und dann resultierende Kraft aus Gewichtskraft und Zentrifugalkraft also FG + 0 ?