Gleichmäßig-Beschleunigte Bewegung

Question

Text erkannt:

Aurgaber:
1. Aulo fährt cincer Bog herveter. Auf \( 4: 4 e 4=150 \mathrm{~m} \) und bé Geschir. \( v_{0}=40 \frac{k \pi}{4} \) versager die Bremsen. Boechue \( v \) ain Fu \( \beta \) des Berges, wame \( a=0,1 \) g sind.
Bechuse die Strigung der Strabe in \( \% \).

Text erkannt:

\( \begin{array}{ll}s(t)=\frac{1}{2} a \cdot t^{2}+v_{0} t+s_{0} & s_{0}=\text { Startpostion } \\ v(t)=a t+v_{0} & v_{0}=\text { Anfangsgeschwirdighed } \\ a(t)=a_{0} & a_{0}=\text { Konstate Besd, langus }\end{array} \)

Problem/Ansatz:

Ich verstehe nicht wie ich rechnen soll.

Comments

merkwürdige Aufgabe. Sind das alle Informationen? Könntest du die Aufgabe abfotografieren?

Ohne Reibung ergibt sich die Beschleunigung a=0,1g aus der Hangabtriebskraft, F_A=m·g·sin(α).

Allgemein ist F=m·a. Daraus kann dann α und somit die Steigung berechnet werden.

---

Das Bild oben ist die Aufgabe so wie sie uns der Lehrer gegeben hat

Answer 1

Hallo

 1. Schritt a gegeben=g/10, (g wie ihr es verwendet) 40km/h in m/s umrechnen Ergebnis v1

dann 150m=v1*t+a/2*t^2 daraus t ausrechen, dann in v=v1+a*t einsetzen ergibt die  gesuchte v (eventuell wieder in km/h umrechnen )

b)0,1g=g*sin(α) daraus sin(α) daraus α  (benutzt: Hangabtriebskrft, m kürzt sich

Gruß lul

Comments

Komme ungefähr auf eine Endgeschwindigkeit von 59 km/h am Fuß des Berges. Stimmt das?

---

lul und ich haben unterschiedliche Interpretationen der Aufgabe. Lul nimmt 150 m als Strecke an, ich 1497,5 m. Mit keinem Ansatz komme ich auf dein Ergebnis. Kannst etwas hochladen?

---

Komme doch auf ein anderes Ergebnis: 73,58km/h

Lade die Rechenweise hoch

---

Ist das richtig?

---

ja, 73,58 km/h ist richtig für die Strecke s=150 m

Answer 2

mit den gegebenen Parametern ist die Aufgabe nur sinnvoll zu lösen, wenn die Reibung und der Luftwiderstand des Autos vernachläßigt werden.

Die Hangabtriebskraft F_A beschleunigt das Fahrzeug. F_A=m·g·sin(α). Allgemein für Kraft und Beschleunigung gilt F=m·a.

Diese beiden Kräft gleichgesetzt erhalten wir

m·a=m·g·sin(α)

m·0,1·g=m·g·sin(α)

sin(α)=0,1

α=5,74°

Die Steigung ist tan(α)·100%=10,05%

Jetzt berechnen wir das rechtwinklige Dreieck um die verbleibenden Strecke s zu berechnen.

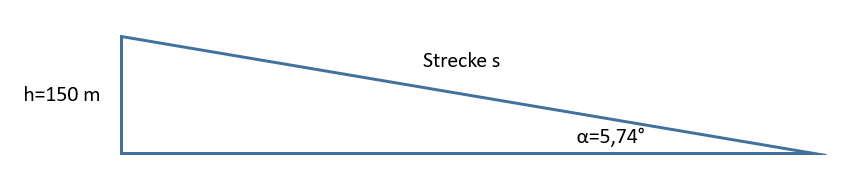sin(α)=h/s

s=1497,5 m

mit v²=v₀²+2·a·s kannst du jetzt die Geschwindigkeit unten am Berg ausrechnen.

Ich komme auf 199,19 km/h.

Zusatzinfo:

- bitte rechne das noch einmal nach

- beachte die Umrechnung der Geschwindigkeit von km/h in m/s und umgekehrt

- das gezeigte Dreieck ist nicht maßstabsgetreu

Comments

Karl hat recht, ich habe Höhe mit Strecke verwechselt, da ohne Reibung gerechnet wird kann man dann mit dem Energiesatz rechnen:

m/2v1^2+mgh=m/2v2^2  m kürzt sich v2^2=2gh+v1^2

damit kommt man auf 194,..km/h

deine Rechnung mit der 150 m Strecke scheint richtig, also mein Fehler beim lesen, sorry