Hallo Christiank,
hier die Antwort zu deiner Frage:
Ist \(\large U_{CD}\) dann \(\large U_{2} - U_{1} = 60V?\) : Nein
Die Vorgabe lautet, den Strom \(\large I_{AB}\) mit Hilfe der Ersatzspannungsquelle bezüglich der Punkte A –B zu berechnen.
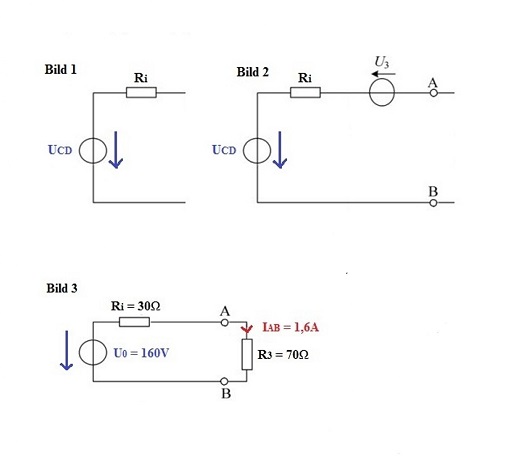
Hierzu berechnet man in einem Zwischenschritt zuerst eine Ersatzspannungsquelle bezüglich C und D mit der Leerlaufspannung \(\large U_{CD}\) und ihrem Innenwiderstand \(\large R_{i}\) (Bild 1).
Anschließend wird zu dieser Ersatzspannungsquelle die Spannungsquelle \(\large U_{3}\) addieret (Bild 2) und man erhält die gesuchte Ersatzspannungsquelle \(\large U_{0}\) mit \(\large R_{i}\) (Bild 3).
 Berechnung von \(\large U_{CD}\):
Berechnung von \(\large U_{CD}\):
Zur Berechnung für \(\large U_{CD}\) muss zunächst der Strom in der Masche M berechnet werden:
Der Strom in der masche M beträgt
\(\large I_{} = \frac{4}{9}A = 0,444A\)
\(\large U_{R2} = I*R_{2} = 20V\)
\(\large U_{CD} = U_{2}+20V = 80V\)
Berechnung des Innenwiderstandes \(\large R_{i}\) :
\(\large R_{i} = R_{1}\vert\vert R_{2} = 30Ω\)
Berechnung der Ersatzspannungsquelle \(\large U_{0}\):
\(\large U_{0} = U_{CD} + U_{3} = 160V\)
Der Innenwiderstand ist unverändert 30Ohm. Damit kann \(\large I_{AB}\) berechnet werden:
\(\large I_{AB} = \LARGE\frac{U_{0}}{R_{i}+R_{3}} = \large 1,6A\)