Hallo,
R2 lässt sich wie folgt sehr einfach berechnen:
1) Beide Stromquellen in Spannungsquellen umrechnen.
2) Die beiden so berechneten Spannungsquellen und die Spannungsquelle U bilden eine Masche.
3) der Strom in dieser Masche lässt sich zu 0,54166 A berechnen
Daraus lässt R2 zu 33,4615 Ohm berechnen.
Alles klar?
Gruß von hightech
Hier als Eränzung die ausführliche Berechnung:
Die Stromquelle Iq1 mit R4 in eine Spannungsquelle Uq1 mit dem Innenwiderstand R4 umrechnen:
\(\large U_{q1} = I_{q1}*R_{4} = 18V\)
Ebenso Iq2 mit R3 in Uq2 mit R3 umrechnen:
\(\large U_{q2} = I_{q2}*R_{3} = 1,5V\)
Durch Umzeichnen erhält man die Schaltung im Bild unten:
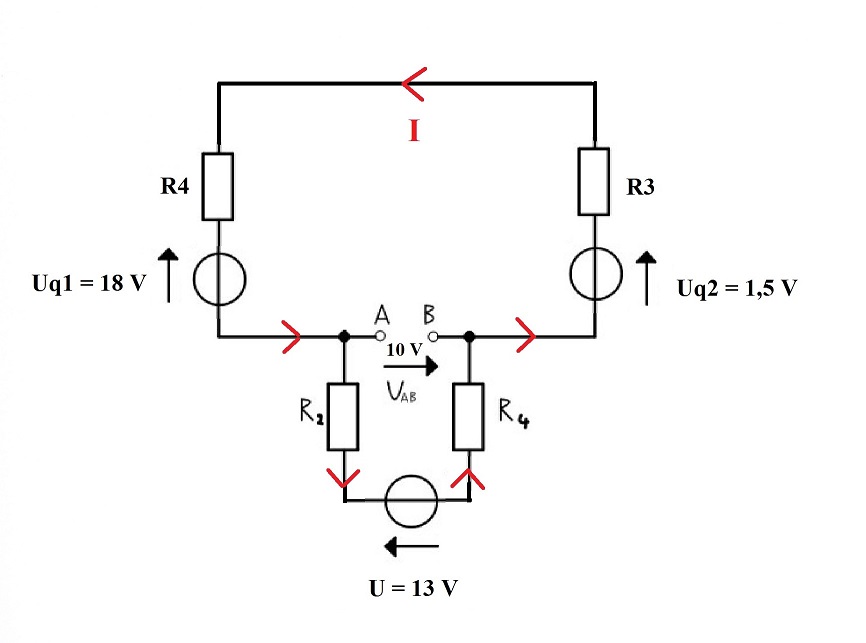
Der Strom I lässt sich allgemein über den äußeren Maschenumlauf berechnen:
I ist der Quotient aus der Summe aller Spannungsquellen dividiert durch die Summe aller Widerstände
\(\large I = \frac{U_{q1}-U_{q2}+U}{R_{4}+R_{3}+R_{4}+R_{2}}\)
\(\large I = \frac{29,5V}{21Ω+R_{2}}\) (Gleichung 1)
Der "kleine" Maschenumlauf unten in der Schaltung liefert:
\(\large I*R_{2}-13V+I*R_{4}-10V = 0\)
umgestellt nach I
\(\large I = \frac{23V}{R_{2}+9Ω}\) (Gleichung 2)
I aus Gleichung 1 mit I aus Gleichung 2 gleichsetzen und nach R2 auflösen
\(\large \frac{29,5V}{21Ω+R_{2}} = \frac{23V}{R_{2}+9Ω}\)
aufgelöst nach R2
\(\large R_{2} = 33,462Ω\)
Obwohl in der Aufgabe nicht nach dem Strom gefragt wurde, kann I jetzt berechnet werden:
\(\large I = \frac{\text{ Gesamtspannung }}{\text{ Gesamtwiderstand }} = \frac{29,5V}{21Ω+33,462Ω}= 0,5416A\)
Gruß von hightech