Wie kann ich denn dann nun die Lagrangefunktion in den Koordinaten s und φ angeben?

Question

Hallo, es geht um Folgendes:

Ein Vollzylinder soll auf einer schiefen Ebene ohne Schlupf abrollen.

Diese Bewegung kann man einerseits unter Nutzung holonomer Zwangsbedingungen mit Lagrange-Parameter
und andererseits durch Reduktion auf eine generalisierte Koordinate beschreiben.

Hier die Skizze zu dem Problem:

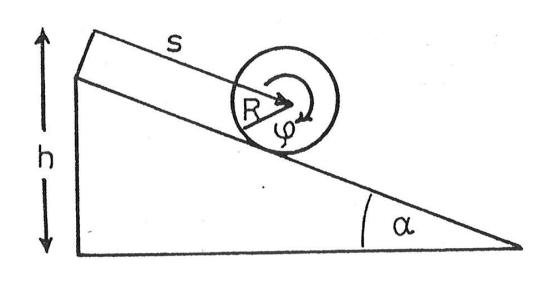
Hierzu soll ich nun die Lagrangefunktion in den Koordinaten s und φ aufstellen. Als Tipp wurde uns gegeben, dass man hierfür die Rotationsenergie eines Zylinders benötigt.

Ich weiß, dass für die Rotationsenergie Folgendes gilt:

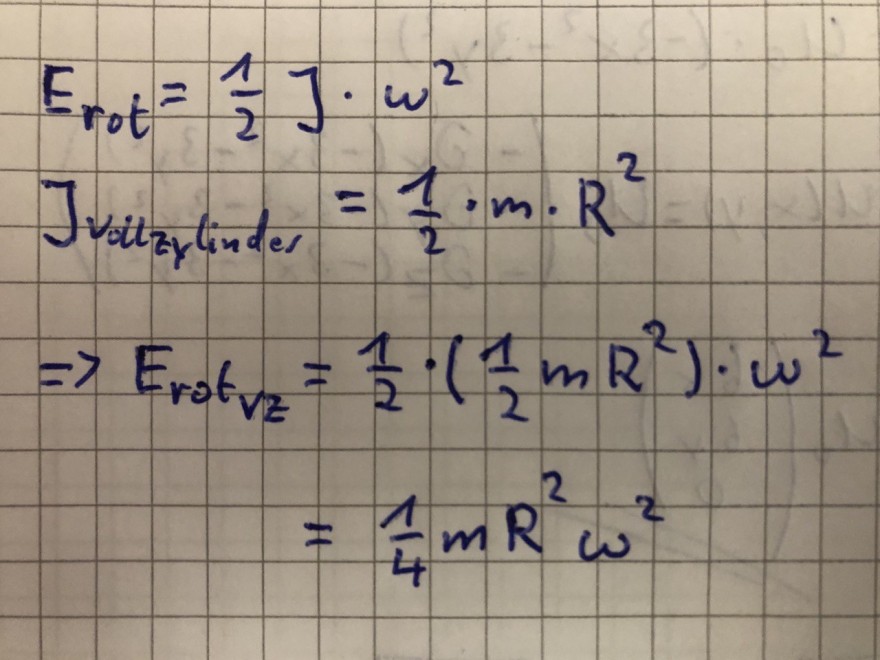
Allerdings ist in der Aufgabenstellung keine Masse m angegeben.

Wie kann ich denn dann nun die Lagrangefunktion in den Koordinaten s und φ angeben?

Welche Zwangsbedingung kann ich hierbei Formulieren und wie würde die Euler-Lagrange-Gleichung dann mit besagter Zwangsbedingung ausformuliert aussehen?

Wäre für jeden Tipp und Hinweis dankbar!

Answer 1

Hallo,

L = T - V

T = E_kin

V = E_pot

Als Tipp wurde uns gegeben, dass man hierfür die Rotationsenergie eines Zylinders benötigt.

Wenn du aber nur die Rotationsenergie berücksichtigst, d.h. die Drehung des Zylinders um seine Zentralachse, dann würde der Schwerpunkt des Zylinders in Ruhe bleiben, d.h. der Zylinder würde nicht die schiefe Ebene hinunter rollen. Es ergibt sich also eine zur Drehung zusätzliche Bewegung (Translation) über den Vektor s(t).

Dementsprechend ist:

T = E_kin = E_rot + E_trans = 0,25 * m * R² * ω + 0,5 * m * v² = 0,25 * m * R² * φ' + 0,5 * m * s'²

Allerdings ist in der Aufgabenstellung keine Masse m angegeben.

Nach Aufstellung der Lagrange-Gleichung sollte sich m weg kürzen lassen.

Einen Vektorpfeil und Ableitungspunkte, anstatt Ableitungsstriche musst du dir denken. ;-)

Comments

Vielen Dank!!! :)