Aufgabe:
Text erkannt:
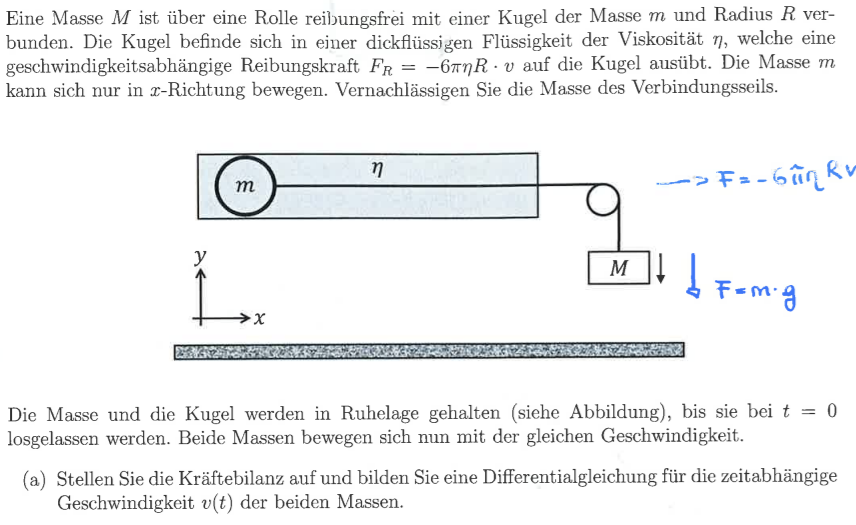
Eine Masse \( M \) ist über eine Rolle reiloungsfrei mit einer Kugel der Masse \( m \) und Radius \( R \) verbunden. Die Kugel befinde sich in einer dickflüssigen Flüssigkeit der Viskosität \( \eta \), welche eine geschwindigkeitsabhängige Reibungskraft \( F_{R}=-6 \pi \eta R \cdot v \) auf die Kugel ausübt. Die Masse \( m \) kann sich nur in \( x \)-Richtung bewegen. Vernachlässigen Sie die Masse des Verbindungsseils.
Die Masse und die Kugel werden in Ruhelage gehalten (siehe Abbildung), bis sie bei \( t=0 \) losgelassen werden. Beide Massen bewegen sich nun mit der gleichen Geschwindigkeit.
(a) Stellen Sie die Kräftebilanz auf und bilden Sie eine Differentialgleichung für die zeitabhängige Geschwindigkeit \( v(t) \) der beiden Massen.
Problem/Ansatz:
Ich weiß nicht wie ich hier die Diff.-gleichung aufstellen soll. Wir haben das bis jetzt nur beim freien Fall behandelt.
Die Reibung von m wirkt ja nur in x-Richtung.
α = -6πηR
=> m*a = -αv
Aber wie spielt dann die Masse M da rein? Nimmt man hier an, dass M*g gilt?
Also:
m*a = -αv-M*g