Berechnen von Stromdichte , Feldstärke und Potenzial(u. Skizze)

Question

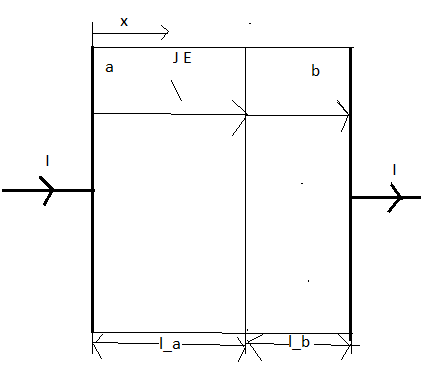
Aufgabe:

Zwei leitfähige Materialen (γa = 100 S/m; l_a = 5 mm;
γ_b = 200 S/m l_b = 3 mm) werden vom Gleichstrom I = 1 A
durchflossen. Die Leiterfläche beträgt 5 mm²

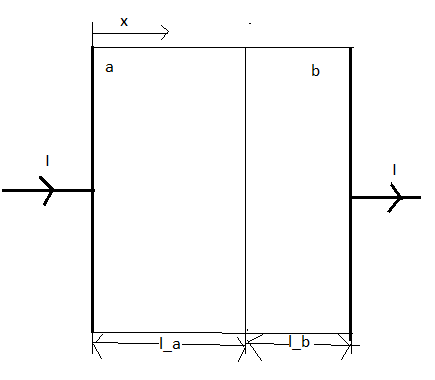
1)Berechnen Sie die Stromdichte und die Feldstärke in beiden
Materialien.

2)Berechnen Sie das Potential in beiden Materialien, wenn die
rechte Elektrode als Bezugselektrode gewählt wird.

3)Skizzieren Sie die Feldverteilung in beiden Materialien.

Problem/Ansatz:

1) I= J*A <=> J= I/A => J = 1A/5mm² = 0,2A/mm² [V]

J_a und J_b sind stetig und E_a und E_b sind stetig.

U= E*l

J= γ*E

J_a = J_b

E = J/γ

E_a = J/γ_a => 0,2V/100 S/m = 0,002Vm/S      E_b=J/γ_b => 0,2V/200 S/m = 0,001Vm/S

Warum kriege ich da 0,002 und nicht 2 und bei E_b 0,001 statt 1 raus?

2)φ_2 - φ_1 = U_21 = E*l_21

0,002Vm/S*(5mm-3mm) = 0,002Vm/S * 2mm = 0,004Vm/S

0,001Vm/S*(5mm-3mm) = 0,001Vm/S * 2mm = 0,002Vm/S

3) 

Answer 1

Hallo,

Du schon wieder   ;-)

Berechnen Sie die Stromdichte und die Feldstärke in beiden Materialien.

Warum kriege ich da 0,002 und nicht 2 und bei E_b 0,001 statt 1 raus?

weil \(\text{mm} \ne \text m\) ist. Du hast fröhlich unterschlagen, dass Du die Stromdichte in \(\text A/\text{mm}^2\) berechnet hast. Und anschließend nur den Zahlenwert eingesetzt hast. Es ist$$J_a = 0,2\,\frac{\text A}{\text{mm}^2} = 2\cdot 10^5\,\frac{\text A}{\text{m}^2} \\ E_a = \frac{J_a}{\gamma_a} = \frac{2\cdot 10^5\,\frac{\text A}{\text{m}^2}}{100\,\frac{\text S}{\text m}} = 2000 \frac{\text V}{\text m} = 2\frac{\text V}{\text{mm}}$$Tipp: in der Physik IMMER die Einheiten mit nehmen.

0,002Vm/S*(5mm-3mm) = 0,002Vm/S * 2mm = 0,004Vm/S

genauso hier: Ohne zu wissen, was Potential ist, sieht man, dass dies nur falsch sein kann. Die \(\text{mm}\) sind hier einfach verschwunden.

Comments

Vielen Dank :)