Aufgabe Kraft:
Eine Last \( F_{G}=3500 \mathrm{~N} \) soll durch eine Konstruktion mit minimalem Kraftaufwand angehoben werden. Der Träger hat ein Eigengewicht von \( 150 \mathrm{~N} / \mathrm{m} \).
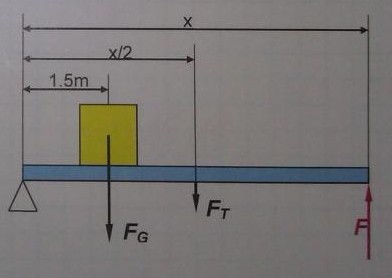
a) Berechne \( \mathrm{F}_{\mathrm{T}} \).
b) Berechne die ideale Länge des Trägers.
Hinweis: Nach dem Momentensatz gilt: \( \mathrm{F}_{-} \mathrm{x}=1,5 \cdot \mathrm{F}_{\mathrm{G}} + \mathrm{F}_{\mathrm{T}} = 0,5 \cdot \mathrm{x} \)
Ansatz/Problem:
Muss ich hier eine Differentialgleichung aufstellen?