Aufgabe:
Die unsymmetrische Dreieckschaltung in Abb. H.2 wird aus einem rechtsdrehenden Drehstromnetz gespeist. Die Außenleiterspannung beträgt \( u_{12}(t)=566 \mathrm{~V} \cos (\omega t) \) bei einer Frequenz \( f=50 \mathrm{~Hz} \). Die Widerstände haben die Werte \( R_{1}=25 \Omega \) \( R_{2}=50 \Omega \) und \( R_{3}=75 \Omega \), die Induktivität beträgt \( L=31,8 \mathrm{mH} \).
a) Berechnen Sie die von der Last aufgenommene gesamte Scheinleistung \( \underline{S} \).
b) Bestimmen Sie die Außenleiterströme \( i_{1}(t), i_{2}(t) \) und \( i_{3}(t) \).
c) Welche Kapazität \( C \) muss ein zwischen \( \mathrm{L}_{1} \) und \( \mathrm{L}_{2} \) geschalteter Kondensator haben, damit die gesamte aufgenommene Blindleistung kompensiert werden kann?
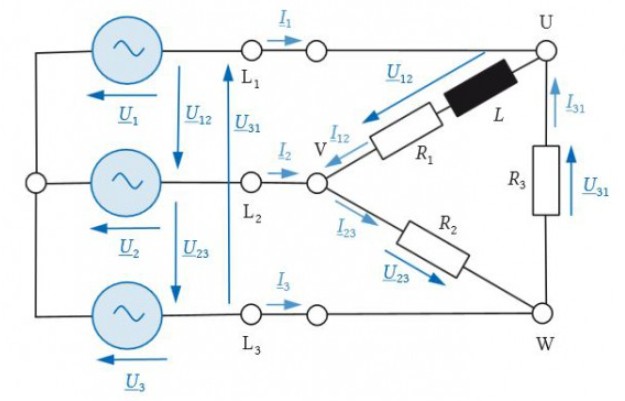
Abbildung: Unsymmetrische Dreieckschaltung
Ansatz/Problem:
Bisher habe ich folgendes gerechnet
Aufgabe a)
\( \begin{aligned} S &=566^{2} v^{2} \cdot\left(\frac{1}{25 \Omega+j^{9,4}}+\frac{1}{50 r}+\frac{1}{75 \pi}\right) \\ &=21902,581-\int 4224,73 A=22306,3 A \cdot e^{-10,9^{\circ}} \end{aligned} \)
Aufgabe b)
