Die Ladung und Entladung eines Kondensators erfolgt entsprechend dem Verlauf einer e-Funktion.
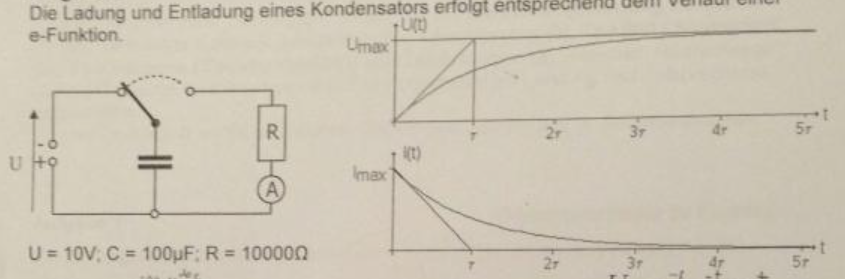
Für die Funktionen des Stroms in Abhängigkeit der Zeit gilt: \( i(t)=\frac{U}{R} \cdot e^{\frac{-l}{R · C} \)
Für die Funktion der Spannung in Abhängigkeit der Zeit gilt: \( u(t)=U \cdot\left(1-e^{\frac{-t}{R \cdot C}}\right) \) Wie in der Grafik zu sehen wird die Zeit in \( \tau \) (Tau) gemessen und mit der Formel
A \( \tau=R \cdot C \) berechnet. Jedoch lässt sich \( \tau \) scheinbar auch durch eine Tangente herleiten.
2.1 Berechnen Sie die Spannungswerte am Kondensator nach \( 0 ; 1 ; 2 ; 3 ; 4 \) und \( 5 \) Sekunden.
2.2 Zu welchem Zeitpunkt ist die Spannung am Kondensator \( 3~V ; 10 ~V ; \) der Versorgungsspannung und \( 50 \% \) einer beliebigen Spannung?
2.3 Beweisen Sie, dass der Grenzwert der Spannung am Kondensator der Versorgungsspannung entspricht.
2.4 Ermitteln und vergleichen Sie die durch beide Methoden ermittelten \( \tau \) -Werte. Verwenden Sie hierfür die Formeln \( { }^{i(t)} \) und \( \tau=R \cdot C\).
2.5 Die Ladungsmenge \( Q(t) \), die sich im Kondensator befindet, entspricht der Fläche unter der Kurve i(t). Bestimmen Sie die Ladung des Kondensators nach 3 Sekunden.