Aufgabe:
Ich muss Aufgabe 1 b) lösen
Text erkannt:
Aufgabe 1
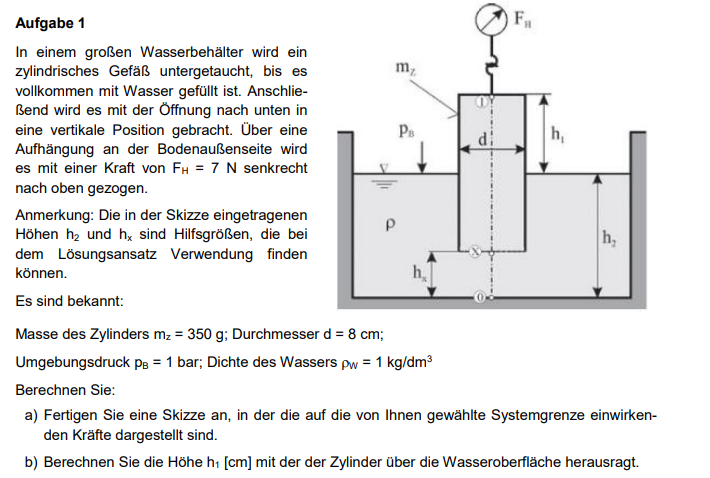
In einem großen Wasserbehälter wird ein zylindrisches Gefäß untergetaucht, bis es vollkommen mit Wasser gefüllt ist. Anschließend wird es mit der Öffnung nach unten in eine vertikale Position gebracht. Über eine Aufhängung an der Bodenaußenseite wird es mit einer Kraft von \( \mathrm{F}_{\mathrm{H}}=7 \mathrm{~N} \) senkrecht nach oben gezogen.
Anmerkung: Die in der Skizze eingetragenen Höhen \( \mathrm{h}_{2} \) und \( \mathrm{h}_{\mathrm{x}} \) sind Hilfsgrößen, die bei dem Lösungsansatz Verwendung finden können.
Es sind bekannt:
Masse des Zylinders \( \mathrm{m}_{\mathrm{z}}=350 \mathrm{~g} \); Durchmesser \( \mathrm{d}=8 \mathrm{~cm} \);
Umgebungsdruck \( \mathrm{p}_{\mathrm{B}}=1 \) bar; Dichte des Wassers \( \rho_{\mathrm{w}}=1 \mathrm{~kg} / \mathrm{dm}^{3} \)
Berechnen Sie:
a) Fertigen Sie eine Skizze an, in der die auf die von Ihnen gewählte Systemgrenze einwirkenden Kräfte dargestellt sind.
b) Berechnen Sie die Höhe \( \mathrm{h}_{1}[\mathrm{~cm}] \) mit der der Zylinder über die Wasseroberfläche herausragt.
Problem/Ansatz:
Das ist mein Ansatz. Das Problem ist, dass ich nicht weiß, wie ich nun auf h_1 kommen soll

Text erkannt:
Aufgabc 1
\( F_{A}=\rho_{F} V^{*} g \quad V^{*}=A \cdot h \)
\( F_{G}=m g \quad A=\frac{\pi d^{2}}{4} \quad h=h_{2}-h_{x} \)
\( \rho_{F} V^{*} g=m g-F_{1 t} \)
\( V^{*}+V_{0}= \) vgen \( \quad V_{\mu}=h_{1}+h_{2}-h \times A \)
\( \operatorname{minh} 2-24 x \cdot A=\ln x=h_{1} A \)