Hallo,
mache Dir ein Bild:
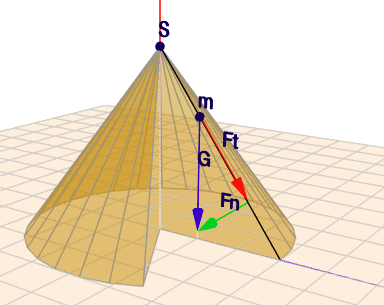
Die Masse \(m\) wird den kürzesten Weg nach unten nehmen, also auf einer Mantellinie des Kegels hinunter rutschen. Die einzige Kraft, die auf sie wirkt, ist die Gewischtskraft \(G\), die sich hier in die Kraft \(F_t\) (tangential) und \(F_n\) (normal) zur Mantellinie aufteilt. Das Verhältnis von \(F_t\) zu \(F_n\) ist wie \(h\) zu \(R\) - dem Radius des Kegels - und daraus folgt auch $$\frac{F_t}{G} = \frac{h}{ \sqrt{h^2+R^2}} \implies F_t = \frac{Gh}{ \sqrt{h^2+R^2}}$$Bezeichne ich mit \(s\) den Weg, den die Masse zurück legt und mit \(v\) ihre Geschwindigkeit so ist$$v = \int \frac{F_t}{m}\, \text dt = \frac{Gh}{ m\sqrt{h^2+R^2}} t + v_0 \\ s = \int v\, \text dt = \frac{Gh}{ 2m\sqrt{h^2+R^2}} t^2 + v_0t + s_0$$ich unterstelle, dass die Anfangsgeschwindigkeit \(v_0=0\) ist. Und da ich \(s\) von der Spitze \(S\) des Kegels zähle, ist auch \(s_0=0\).
Die Pojektion von \(s\) bzw. \(s(t)\) auf die Grundfläche ist der Weg \(r(t)\) der Masse$$r(t) = s(t) \frac{R}{\sqrt{h^2 + R^2}} = \frac{gRh}{2(h^2+R^2)}t^2$$\(g\) steht für die Erdbeschleunigung und weiter gilt \(G=mg\).
Bestimmen sie die Geschwindigkeit am Boden
Der Boden ist erreicht, wenn \(s(t) = \sqrt{h^2+R^2}\)$$\implies t_{\text{end}} = \sqrt{\frac{2(h^2+R^2)}{gh}} \implies v_{\text{end}} = \sqrt{2gh}$$
... und überprüfen sie, ob ihr Ergebnis die Energieerhaltung bestätigt.
nach dem Energieerhaltungssatz, müsste die potentielle Energie \(mgh\) am Anfang gleich der kinetischen Energie \(mv_{\text{end}}^2/2\) am Ende sein, wenn die Masse die Grundfläche des Kegels erreicht. Daraus folgt$$\begin{aligned} mgh &= \frac12 m v_{\text{end}}^2 \\ \implies v_{\text{end}} &= \sqrt{2gh}\end{aligned}$$das stimmt also überein.