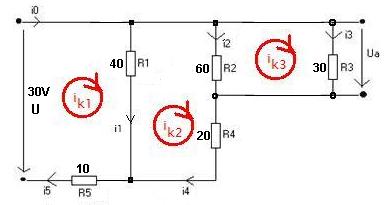
Wie stelle ich die Maschen- & Knotengleichungen auf?
Dein Schaltbild habe ich (in die übliche Form) umgezeichnet, sodass links die Quelle, Ströme von links nach rechts, Maschenströme rechtsherum.
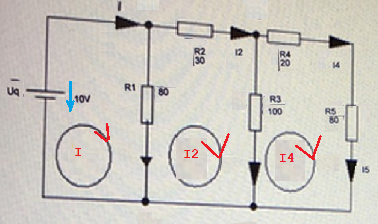
Matrix aufstellen (enthält implizit die Knotengleichungen
I
| I2
| I4
| =
|
R1
| -R1
| 0
| Uq
|
-R1
| R1+R2+R3
| -R3
| 0
|
0
| -R3
| R3+R4+R5
| 0
|
oder mit den eingesetzten Zahlenwerten:
80
| -80
| 0
| 10
|
-80
| 210
| -100
| 0
|
0
| -100
| 200
| 0
|
|
|
|
|
Lösung: I=1/4 A, I2 = 1/8 A, I4 = I5 = 1/16 A
Daraus I1 = I-I2 = 1/8 A und I3 = I2 - I4 = 1/16 A
Wie stellt man die Matrix auf? s. Kochrezept:
Solche Aufgaben löst man zweckmäßig mit dem Maschenstromverfahren. Dabei bewährt es sich, wenn man die Stromrichtung in jeder Masche im Uhrzeigersinn annimmt, denn dann ist die Maschenmatrix nach Kochrezept sehr einfach zu erstellen. Wenn man - was man darf - für jedes Bauteil separat Pfeile festlegt, hat man recht hohe Wahrscheinlichkeit für Fehler.
Hier nochmal die Regeln für das 'Kreisstromverfahren' = Maschenstromverfahren. Vorteile: o Bei sich nicht überschneidenden Maschen und gleichem Kreisstromdrehsinn sind die Regeln simpel. o wenig Unbekannte, ordentliche Darstellung, o leichte Nachprüfbarkeit jeden Schrittes(Doublecheck!) Beispiel Kreisstromverfahren: siehe Bildchen Die Regeln zum Kreisstromverfahren sind: a) die ik1...ik3 Schleifen einzeichnen oder sich denken b) für jede dieser ik-Maschen eine Gleichung aufstellen b1) die Widerstände mit dem eigenen ik sind positiv b2) die Widerstände mit den Nachbar-ik sind negativ b3) Spannungsquellen mit gleichlaufendem Pfeil sind negativ und werden rechts eingetragen b4) Spannungsquellen mit entgegengesetztem Pfeil sind positiv und werden rechts eingetragen c) Die Auflösung der Gleichung nach Gauß-Jordan ergibt die ik1...ik3 c1) wenn man die Zahlen einsetzt, löst Brünner c2) alternativ - auch mit Buchstaben löst TI89 mit rref() c3) natürlich kann man auch von Hand auflösen Beachte: Die ganze Schreibarbeit ist das folgende Codefenster:
R1+R5 -R1 0 U -R1 R1+R2+R4 -R2 0 0 -R2 R2+R3 0
Gauß-Jordan ergibt ik1, ik2, ik3 i0; i1; i3; i4; i5; iges; U1; Ua; i0 = ik1 i1 = ik1-ik2 i2 = ik2-ik3 i3 = ik3 i4 = ik2 i5 = ik1 U1 = i1*R1 Ua = i3*R3
Ergänzend dazu das Knotenpotentialverfahren, es ist dual zum Kreisstromverfahren, d.h. Strom → Spannung Widerstand → Leitwert Masche → Knoten Knoten → Masche Spannungquelle → Stromquelle Ohmsches Gesetz: U = R * I → I = G * U Die Regeln für das Knotenpotentialverfahren sind:
a) die φ1...φ3.. Knotenpotentiale einzeichnen oder sich denken
b) für jede dieser f-Knoten eine Gleichung aufstellen
b1) die Leitwerte mit dem eigenen φ sind positiv
b2) die Leitwerte mit den Nachbar-φ sind negativ
b3) Stromquellen mit Zufluss sind positiv und werden rechts eingetragen
b4) Abfluss natürlich negativ
c) Die Auflösung der Gleichung nach Gauß-Jordan ergibt die φ1...φ3..
c1) wenn man die Zahlen einsetzt, löst Brünner
c2) alternativ - auch mit Buchstaben löst z.B. TI89 mit rref()
c3) Man kann natürlich auch 'von Hand' lösen