Text erkannt:
\( f \)
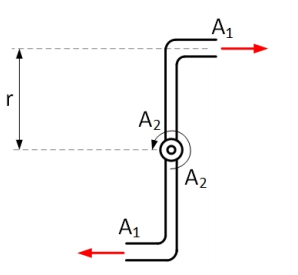
Der in der Draufsicht abgebildete symmetrische Rasensprenger fordert den Volumenstrom \( Q \), der über die
beiden Arme entsprechend der Abbildung ausströmt. Gegeben seien die Querschnitte \( A_{1} \) und \( A_{2}, \) sowie der
Abstand \( r \) und die Dichte \( \rho \) der Flüssigkeit.
Welches Moment wirkt auf den Rasensprenger? Bitte ankreuzen.
[ ] \( M=\frac{Q}{A_{1}} \rho^{2} \)
[ ] \( M=\frac{Q^{2}}{2 A_{1}} \rho r \)
[ ] \( M=\frac{A_{1} A_{2}}{Q^{2} \rho r} \)
[ ] \( M=\frac{2}{3} \frac{Q}{A_{1}^{2}} \rho r \)
[ ] \( M=\frac{1}{3} \frac{\rho}{A_{1} A_{2}} \dot{Q} r \)
[ ] \( M=\dot{Q}^{2} \frac{\rho}{A_{1}} r \)
[ ] \( M=2 \dot{Q}^{2} r \sin \alpha \)
Meine Lösungen:
M=r*F
Wie rechne ich hier jetzt F aus, habe ich die Formel richtig aufgestellt?
F= ρ*A*u2
Ich komme hier leider nicht auf M.
Gruß