Text erkannt:
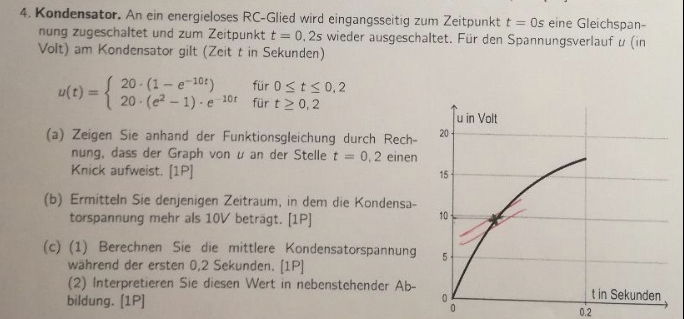
4. Kondensator. An ein energieloses RC-Glied wird eingangsseitig zum Zeitpunkt \( t=0 \) s eine Gleichspannung zugeschaltet und zum Zeitpunkt \( t=0.25 \) wieder ausgeschaltet. Fur den Spannungsverlauf \( u \) (in Volt) am Kondensator gilt (Zeit \( t \) in Sekunden)
\( u(t)=\left\{\begin{array}{ll}20 \cdot\left(1-e^{-10 t}\right) & \text { für } 0 \leq t \leq 0,2 \\ 20 \cdot\left(e^{2}-1\right) \cdot e^{-10 t} \text { für } t \geq 0,2\end{array}\right. \)
(a) Zeigen Sie anhand der Funktionsgleichung durch Rechnung, dass der Graph von \( u \) an der Stelle \( t=0,2 \) einen
Knick aufweist. [1P]
(b) Ermitteln Sie denjenigen Zeitraum, in dem die Kondensstorspannung methr als \( 10 \mathrm{V} \) betragt. (IP]
(c) ( 1) Berechnen Sie die mittlere Kondensatorspannung wahrend der ersten 0.2 Sekunden.
(2) Interpretieren Sie diesen Wert in nebenstehender Ab-
bildung. (1P] in Sekunden
Aufgabe: