Einmal 2 und 3 Massen die über Seile verbunden sind.

Question

Aufgabe:

g = 10 m/s²

m₁ = 1,0 kg

m₂ = 0,5 kg

m₃ = 2,0 kg

Reibung wird vernachlässigt.

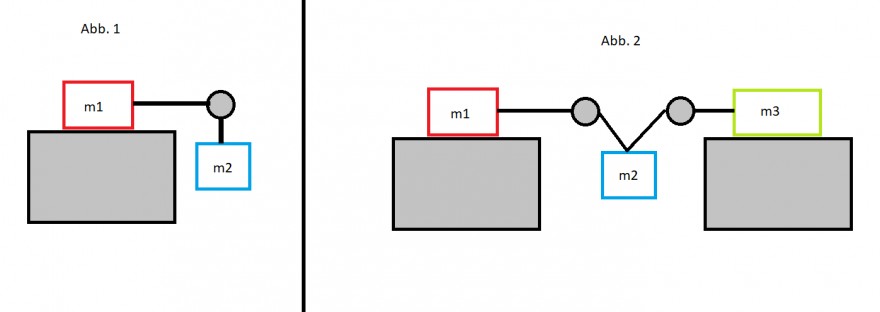
Abb.1)

a) Berechnen Sie, mit welcher Beschleunigung a₁ sich der Massenzug in Bewegung setzt.

b) Nun soll m₁ durch eine andere Masse m₁* ersetzt werden, so dass sich der Massenzug mit a₂ = 5 m/s² in Bewegung setzt. Bestimme m₁*.

Abb. 2)

c) Berechne a₃.

d) Das selbe Experiment wird auf dem Mond durchgeführt. Nach loslassen von m₂ legt es die Strecke Δs = 1m und

Δt = 2,94s zurück. Bestimme g_mond.

Problem/Ansatz:

Ich bin mir nicht sicher ob ich die richtigen Formeln verwende, weil da auch negative Ergebnisse rauskommen.

a)

\( F_{g}=m_{g} \cdot a \)

\( \frac{F_{g}}{m_{g}}=a \)

\( \frac{m_{2} \cdot g-m_{l} \cdot g}{m_{l}+m_{2}}=a \)

\( \frac{0,5 \mathrm{kg} \cdot 10 \frac{\mathrm{m}}{\mathrm{s}^{2}}-1 \mathrm{kg} \cdot 10 \frac{\mathrm{m}}{\mathrm{s}^{2}}}{1 \mathrm{kg}+0,5 \mathrm{kg}}=a=-\frac{10}{3} \frac{\mathrm{m}}{\mathrm{s}^{2}} \)

b)

\( m_{2} \cdot g=\left(m_{1}* ~ m_{2}\right) \cdot a \)
\( \frac{m_{2} \cdot g}{a}=m_{1}* ~ m_{2} \)
\( \frac{m_{2} \cdot g}{a}-m_{2}=m_{1}* \)
\( \frac{0,5 \mathrm{kg} \cdot 10 \frac{\mathrm{m}}{\mathrm{s}^{2}}}{5 \frac{\mathrm{m}}{\mathrm{s}^{2}}}-0,5 \mathrm{kg}=0,5 \mathrm{kg} \)
\( m_{1}* ~ =0,5 \mathrm{kg} \)

c)

\( F_{g}=m_{g} \cdot a \)

\( \frac{F_{g}}{m_{g}}=a \)

\( \frac{g\left(m_{2}-\left(m_{l}+m_{3}\right)\right)}{m_{1}+m_{2}+m_{3}}=a \)

\( \frac{10 \frac{m}{s^{2}}(0,5 k g-(1 k g+2 k g))}{1 k g+0,5 k g+2 k g}=-\frac{50}{7} \frac{m}{s^{2}} \)

d)

\( F_{g}=m_{g} \cdot a \)
\( \frac{F_{g}}{m_{g}}=a \)
\( \frac{g\left(m_{2}-\left(m_{l}+m_{3}\right)\right)}{m_{l}+m_{2}+m_{3}}=a \)
\( a=\frac{s}{t^{2}} \)
\( \frac{1 m}{(2,94 s)^{2}} \cdot \frac{1 k g+0,5 k g+2 k g}{0,5 k g-(1 k g+2 k g)}=g=-\frac{10}{21} \frac{m}{s^{2}} \)

Answer 1

Hallo Nathan,

zu a)

... weil da auch negative Ergebnisse rauskommen

Du schreibst ja nirgends wie das \(a\) definiert ist. Wenn \(a\) die Beschleunig der Massen \(m_1\) nach links und \(m_2\) nach oben ist, so ist \(a = -\frac 13 g\) das richtige Ergebnis. Nur der Rechenweg ist falsch.

Wenn \(a\) die Beschleunigung nach links & oben ist und \(S\) die Zugkraft im Seil, so gilt $$\begin{aligned} -S &= m_1 \cdot a \\ S - G_2 &= m_2 \cdot a \\ \implies - m_1 \cdot a - G_2 &= m_2 \cdot a \\ -m_2 \cdot g &= (m_2 + m_1) a \\ a & = -\frac {m_2}{m_1 + m_2} g = - \frac 13 g\end{aligned}$$Du hattest bloß das Glück, dass \(m_2\) genauso groß ist wie \(m_1 - m_2\).

zu b) hier hast Du es richtig gemacht. Du kannst natürlich auch die Gleichung $$a = \frac{m_2}{\sum m_i} g$$ verwenden (das Minus lasse ich mal weg, dann geht die Beschleunigung mit \(m_2\) nach unten) mit $$a = 0,5 \frac{\text m}{\text s^2} \approx \frac 12 g = \frac{m_2}{\sum m_i} g$$sieht man, dass \(\sum m_i = m_1^* + m_2 = 2 m_2\) sein muss. Also ist \(m_1^* = m_2\)

c) hier hättest Du merken müssen, dass etwas nicht stimmt \(\frac{50}7 \gt 7\) d.h. die Beschleunigung ist größer als vorher, obwohl mehr (bremsende) Masse auf dem Tisch liegt und das gleiche \(m_2\) daran zieht. Das macht keinen Sinn.

Benutze wieder die Gleichung von oben $$a = \frac{m_2}{\sum m_i} g = \frac{0,5}{1,0 + 0,5 + 2,0} g = \frac 17 g$$Du siehst, die Beschleunigung wird deutlich kleiner.

d) Nutze wieder die gleiche Formel nur diesmal mit der Fallbeschleunigung \(g_{\text{Mond}}\) auf der Mondoberfläche$$a = \frac 17 g_{\text{Mond}}$$Weiter gilt $$\begin{aligned} s &= \frac 12 a t^2 \\ 1 \,\text m &= \frac 12 \cdot \frac 17 g_{\text{Mond}} \cdot \left( 2,94 \,\text s\right)^2 \\ \implies g_{\text{Mond}} &= \frac{2 \cdot 7}{ 2,94^2} \frac{\text m}{\text s^2} \approx 1,62 \frac{\text m}{\text s^2}\end{aligned}$$ Schlag nach bei Wiki - das kommt hin.

Gruß Werner