Zwei Massen m1 und m2 (m2 > m1) können sich im Schwerefeld der Erde auf um die Winkel
α und β gegen die Horizontale geneigten Ebenen reibungslos bewegen. Sie sind durch einen
masselosen Faden der konstanten Länge l miteinander verbunden.
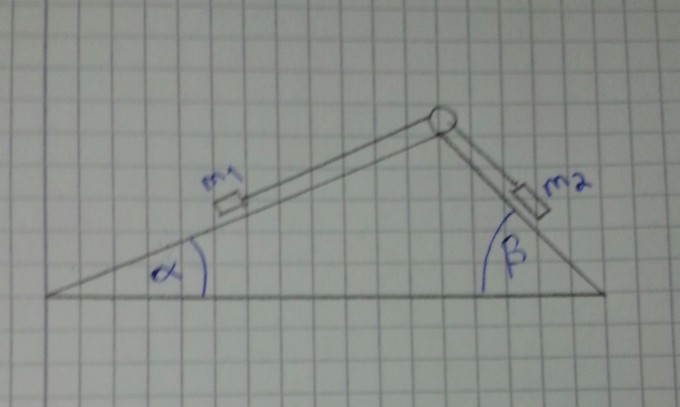
a) Führen Sie eine generalisierte Koordinate q zur Beschreibung der quasi eindimensionalen
Bewegung ein und legen Sie fest, in welche Richtung die Koordinate
q zeigt.
b) Betrachten Sie die Anordnung aus den beiden Massen und dem Faden zunächst als drei
Körper: Summieren Sie für die Masse m1 alle auf sie wirkenden Kräfte (Oberflächenund
Volumenkräfte) und stellen Sie unter Anwendung des zweiten Newtonschen
Axioms die Bewegungsgleichung für die Masse m1 auf. Stellen Sie ebenso die
Bewegungsgleichung für die Masse m2 auf.
c) Zeichnen Sie alle auf den Faden wirkenden Kräfte ein. Identifizieren Sie mithilfe des
dritten Newtonschen Axioms Kräfte, die betragsmäßig gleich sind und sich nur durch
ihre Richtung unterscheiden.
d) Da alle drei Körper miteinander verbunden sind werden Sie mit derselben
Beschleunigung beschleunigt. Lösen Sie das obige Gleichungssystem und stellen Sie
eine Formel auf, mit der die Beschleunigungen der gesamten Anordnung aus den
Größen α,β, der Erdbeschleunigung g, m1 und m2 berechnet werden kann.
e) Geben Sie die Bedingung an, unter der sich die Massen in Ruhe oder in gleichförmig
geradliniger Bewegung (bezogen auf die generalisierte Koordinate) befinden.
Ich fühle mich aktuell, erwas überfordert... :(