Schwingfähiges System : Wie lautet die Differentialgleichung für die Rotationsschwingung der Punktmasse um A?

Question

Ein schwingfähiges System besteht aus zwei starren, masselosen Stäben, die im Punkt A gelenkig gelagert
sind, einer Punktmasse, zwei Federn, einer Torsionsfeder, sowie einem Dämpfer. Das System wird anfangs um einen kleinen Winkel ausgelenkt und dann sich selbst überlassen. Wie lautet die Differentialgleichung für die
Rotationsschwingung der Punktmasse um A?

Text erkannt:

WhW
WWW
CT
CT
d \( \frac{1}{\text { d }} \frac{1}{\text { A }} \)
5 \( \quad \) S \( \quad \) S \( \quad \) S \( \quad \) S \( \quad \) S \( \quad \) S

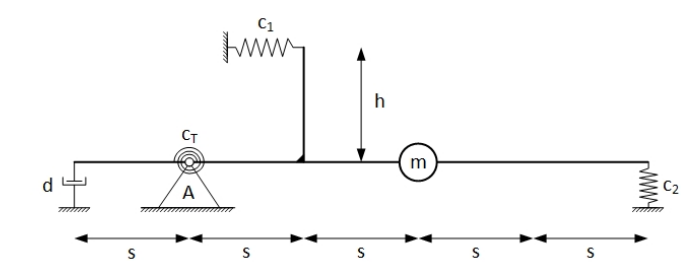
 Abbildung 4: Skizze eines schwingfähigen Systems: Die Punktmasse m, die Längen (h und 5s), die Steifigkeiten

(c1 6 ≠ c2), die Torsionssteifigkeit (cT ) und die Dämpfungskonstante (d) sollen als bekannt betrachtet werden.

Wie kann man solche Aufgaben am einfachsten lösen?

Answer 1

Hallo

 man addiert die 3 rücktreibenden Kräfte von c1,c2,ct, bzw das Drehmoment das sie auf m ausüben.

da die Ausrenkung klein ist ist die Längenänderug der Federn c2: 4s*φ,  c1: s*φ

Gruß lul

Comments

einfach nur addieren so einfach war das?

4s*φ+s*φ+ct

---

 zu ct noch phi

 dann noch die Dämpfung und dann  musst du natürlich noch die Gleichung aufstellen. am besten mit Drehmoment um A aus den Kräften  um A und I*phi''.