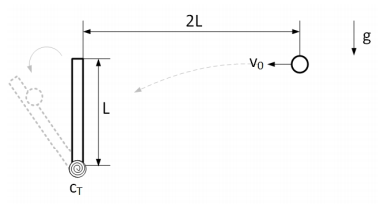
Auf den dargestellten masselosen Hebel der Länge L wird eine Kugel der Masse mk mit der Anfangsgeschwindigkeit v0 aus der Entfernung 2L horizontal in Richtung des Hebels geworfen. Die Kugel kann hierbei als
Massenpunkt idealisiert werden. Der Einschlag der Kugel auf den Hebel erfolge vollplastisch, so dass sich
Hebel und Kugel nach dem Einschlag gemeinsam um den Lagerpunkt drehen. Im Lagerpunkt ist eine Torsionsfeder mit der Federsteifigkeit cT am Hebel angebracht. Es wirke eine Gravitationsbeschleunigung von g in
der eingezeichneten Richtung senkrecht zu v0. Gegeben sind g ∼ 10m/s^2, v0 ∼ 10m/s, L = 1m, cT = 2500 Nm
und mk = 25 kg.
An welchem Punkt yP längs des Hebels trifft die Kugel auf? Nehmen Sie hierfür an, dass der Lagerpunkt y0 = 0 m entspricht und nach oben hin positiv gezählt wird.
[ ] yP = L/2,
[ ] yP = L/3,
[ ] yP = 3L/5,
[x] yP = 4L/5,
[ ] yP = 2L/3.
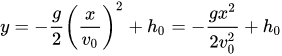 = -10/2m/s^2*(2.1/10 m/s)+1 m = 0,8 m=4/5 L
= -10/2m/s^2*(2.1/10 m/s)+1 m = 0,8 m=4/5 L
Welche Winkelgeschwindigkeit haben Kugel und Hebel gemeinsam nach dem Aufprall der Kugel, wenn der
vertikale Anteil der Kugelgeschwindigkeit vor dem Aufprall vernachlässigt werden kann?
[ ] ω = 5 rad/s,
[ ] ω = 7, 5 rad/s,
[ ] ω = 12, 5 rad/s,
[ ] ω = 15 rad/s,
[ ] ω = 20, 5 rad/s,
Welche Formel muss ich hier anwenden?
Wie weit lenkt sich der Hebel inklusive Kugel aus, wenn nach dem Aufprall der Einfluss der Gravitation
vernachlässigt werden kann ?
[ ] φ = 0, 1 rad,
[ ] φ = 0, 5 rad,
[ ] φ = 1, 0 rad,
[ ] φ = 1, 5 rad,
[ ] φ = 2, 0 rad,
Und hier weiß ich auch nicht wie ich auf die Lösung komme, wahrscheinlich muss ich erst die Winkelgeschwindigkeit berechnen....?