Stützkräfte berechnen Mechanik

Question

Hallo zusammen,

ich stehe bei folgender Aufgabe ziemlich auf dem Schlauch:

Ein unbelasteter Stab liegt in den Punkten A und B reibungsfrei auf. Im Abstand l1=2m vom Punkt B wirkt seine Gewichtskraft FG=100N. Die anderen Abstände betragen l2=3m und l3=1m.

Gesucht:

a) Die Stützkraft FA und ihre Komponenten FAx und FAy

b) Die Stützkraft FB und ihre Komponenten FBx und FBy.

Ich weiß nicht genau wie das mit dem Copyright ist, daher füge ich an dieser Stelle mal keine Skizze an. Die Aufgabe (und auch die Lösung) lassen sich aber recht einfach finden: Einfach den ersten Satz der Aufgabe in die Suchmaschine des Vertrauens einfügen. Man landet dann bei der Aufgabe 103 in der Aufgabensammlung für technische Mechanik.

Bei mir hakt es an erster Stelle gleich beim Aufstellen der drei Gleichgewichtsgleichungen.

$$\sum \limits_{}^{} F_x = 0 = F_Ax - F_Bx$$

$$\sum \limits_{}^{} F_y = 0 = F_Ay + F_By - F_G$$

$$\sum \limits_{}^{} M_B = 0 = -F_Gl1 + F_A sina *l2 + F_Acosa *l3$$

Ich verstehe vor allem die 3. Gleichung nicht. Wieso rechnet man z.B. -FG*l1 und FA*sin*l2 ?

Ich dachte den Sinus nimmt man für y-Achse und den Kosinus für die x-Achse?

Wäre super, wenn mir da jemand helfen könnte. Wie gesagt, die Lösung ist auch im Internet zu finden und auch mit der versteh ich's einfach nicht wirklich.

Answer 1

Hallo, 

ich schreibe Vektoren fett    (z.B. F_A  ,  F_A ist dann der Betrag der Kraft )

Ich verstehe vor allem die 3. Gleichung nicht. Wieso rechnet man z.B. -FG*l1 und FA*sin*l2 ?

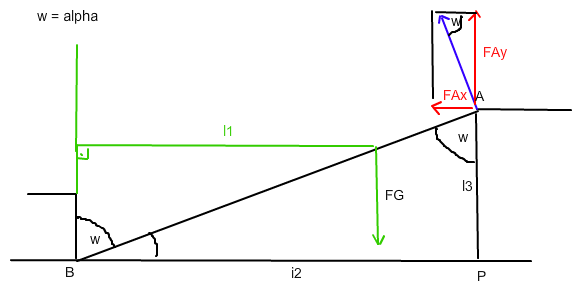
Der Winkel  α bei B ist in der Zeichnung mit w bezeichnet und dieser kommt dann aus geometrischen Gründen noch an anderen Stellen in der Zeichnung vor. 

Im Δ_BPA  gilt:   tan(α) = l₂ / l₃  →  α

Die Kraft F_A  (blau)  wirkt vom Punkt A aus senkrecht zum Balken schräg nach links oben.

Im Kräfteparallelogramm oben rechts gilt: 

sin(α) = F_Ay / F_A  und  cos(α) = F_Ax / F_A

→  F_Ay = F_{A ·} sin(α)  und  F_Ax = F_A · cos(α)

F_Ax wirkt nach links  und F_Ay nach oben. Beide bewirken ein Drehmoment gegen den Uhrzeigersinn (positive Drehrichtung)

F_G bewirkt ein rechtsdrehendes Drehmoment, daher  - F_G

Die wirksamen Hebelarme für die Drehmomente der Kräfte: 

Stell dir vom Angriffspunkt der jeweiligen Kraft aus das Lot zur Parallelen der Wirkungsrichtung der Kraft durch B vor. Die Länge dieses Lotes ist jeweils der wirksame Hebelarm der Kraft. ( Für F_G  habe ich das mal grün eingezeichnet: wirksamer Hebelarm = l₁ )

→    l₃  für  F_Ax und  I₂  für  F_Ay 

In Gleichung III steht eigentlich  $$ \sum\limits_{}^{} M_B=0=-F_G·l_1+\color{blue}{F_{Ay}·l_2}+\color{blue}{F_{Ax}·l_3}$$wobei das Drehmoment der Kraft  F_A durch die Summe der Drehmomente ihrer Komponenten ersetzt ist.

Danach wurden diese Komponenten dann wie oben ersetzt und es entstand Gleichung III

In III hast du nur noch die Unbekannte F_A , die du ausrechnen kannst. 

Aus  diesen  obenstehenden  Gleichungen   →   F_Ax , F_Ay 

 Aus I und II ergeben sich dann  F_Bx und F_By  und mit Pythagoras F_B

Gruß Wolfgang                                                                                                                              

Comments

Erst einmal danke für deine Antwort!

FAx wirkt nach links  und FAy nach oben. Beide bewirken ein Drehmoment gegen den Uhrzeigersinn (positive Drehrichtung)

Bis hierhin komme ich mit. Nur das mit den Hebelarmen für die Drehmomente bereitet mir noch Kopfzerbrechen :(

---

Stell dir jeweils eine Parallele durch den Drehpunkt B zu der Wirkungsrichtung der Kraft vor. Die Länge des Lots dazu vom Angriffspunkt der Kraft aus ist deren wirksamer Hebelarm.

Für  F_G  habe ich das grün eingezeichnet  →  l₁

Habe das Bild noch etwas ergänzt.

---

Dann ist meine gedachte Parallele quasi FG und deren Hebelarm l1 ?

Aber wie ist das mit l2 und l3 ? Und wieso gilt für die anderen beiden Drehmomente sina*l2 und cosa*l3 ?  

---

Letzteres sind nicht die Hebelarme!

Bei   F_A · sin(α) · l₂ 

 ist     das F_Ay  und  das der Hebelarm  für F_Ay 

Das wirksame Drehmoment der Kraft  F_A  ist in  Gleichung III für seine Berechnung 

durch die Summe der wirksamen Drehmomente 

ihrer Komponenten  F_Ay  und  F_Ax  ersetzt.

(leider nicht in alphabetischer Reihenfolge, was auch mich zeitweise verwirrt hat)

---

Ich glaube ich muss mich erstmal hinlegen. Heute krieg ich nix gscheites mehr hin.  xD

---

Tu das, lies aber zuerst noch meine letzte Ergänzung im vorhergehenden Kommentar :-)

---

Das habe ich auch soweit verstanden (glaube ich). Nur verstehe ich nicht die Verknüpfung zwischen l₂ und F_AY .

Für y gilt sin a.

Nur l₂ liegt doch auf x...

Stell dir jeweils eine Parallele durch den Drehpunkt B zu der Wirkungsrichtung der Kraft vor. Die Länge des Lots dazu vom Angriffspunkt der Kraft aus ist deren wirksamer Hebelarm.

Ich glaube das muss ich mir morgen nochmal in Ruhe durch den Kopf gehen lassen.

Trotzdem schonmal Danke für deine Bemühungen :)

---

@ Lampenschirm

Habe die Antwort für dich noch einmal bearbeitet und hoffe, dass du sie jetzt besser verstehst.

---

Erstaunlich, was ein paar Stunden Schlaf ausmachen...

Heute rangesetzt, einmal kurz drübergeschaut: *Klick*

Vielen Dank noch einmal und noch einen schönen Sonntag! :-)

---

immer wieder gern :-)

Answer 2

hallo

du hättest ja direkt den link Angebern können.

Drehmoment=Kraft *Abstand  zur Wirkungslinie der Kraft, der Abstand wird durch Länge* sin bzw cos bestimmt, das hat nix mit x und y Richtung zu tun.

Welches der Drehmomente du positiv, welches negativ rechnest ist egal. die Hauptsache links und rechtsdrehend haben entgegengesetzte Vorzeichen, FA und FB müssen ja das Gegendrehmoment aufbringen.

so klarer?

Gruß lul

Comments

Leider nicht ganz.. Das mit den Drehmomenten macht mir noch Schwierigkeiten :(

---

 dann schreib mal wie du z.B das Drehmoment bei A bestimmst wenn Fa bekannt ist.

---

Hat sich geklärt s.o. :-)